참고 서적
 |
도서명: 모두의 딥러닝 저자 : 조태호 출판 : 길벗 발매 : 2020.01.27 |
오차 역전파
신경망 내부의 가중치는 오차 역전파 방법을 사용해 수정한다. 오차 역전파는 경사 하강법의 확장 개념이다.
우리는 XOR 문제를 해결할 때 정답에 해당하는 가중치와 바이어스를 미리 알아본 후 이를 집어넣었다. 그렇다면 이 가중치와 바이어스를 실제 프로젝트에서는 어떻게 구할 수 있을까? 이 부분은 어려운 문제이기도 하고, 딥러닝으로 나아가는 가장 중요한 부분이기도 하다.
우리가 앞서 배운 경사 하강법은 임의의 가중치를 선언하고 결괏값을 이용해 오차를 구한 뒤 이 오차가 최소인 지점으로 계속해서 조금씩 이동시킨다. 이 오차가 최소가 되는 점(미분했을 때 기울기가 0이 되는 지점)을 찾으면 그것이 바로 우리가 알고자 하는 답이다. 하지만 경사 하강법은 입력과 출력이 하나인 '단일 퍼셉트론' 일 경우에 사용한다.
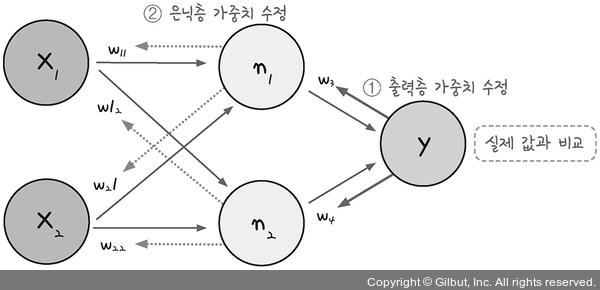
다층 퍼셉트론 역시 결괏값의 오차를 구해 이를 토대로 하나 앞선 가중치를 차례로 거슬러 올라가며 조정해 나간다. 그러다보니 최적화의 계산 방향이 출력층에서 시작해 앞으로 진행된다. 그래서 다층 퍼셉트론의 최적화 과정을 오차 역전파(back propagation)라고 부른다.
오차 역전파의 구동 방식은 다음과 같다.
- 임의의 초기 가중치(w)를 준 뒤 결과(y)를 계산한다.
- 계산 결과와 우리가 원하는 값 사이의 오차를 구한다.
- 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트 한다.
- 위 과정을 더이상 오차가 줄어들지 않을 때까지 반복한다.
'오차가 작아지는 방향으로 업데이트 한다.'는 의미는 미분 값이 0에 가까워지는 방향으로 나아간다는 말이다. 즉, '기울기가 0이 되는 방향'으로 나아가야 하는데, 이 말은 가중치에서 기울기를 뺐을 때 가중치의 변화가 전혀 없는 상태를 말한다. 따라서 오차 역전파를 다른 방식으로 표현하면 가중치에서 기울기를 빼도 값의 변화가 없을 때까지 계속해서 가중치 수정 작업을 반복하는 것이다.

편미분 과정 유도
yo1 - yt1로 편미분되는 과정을 유도하면 다음과 같다.





입력된 실제 값과 다층 퍼셉트론의 계산 결과를 비교하여 가중치를 역전파 방식으로 수정해 가는 코딩은 다음과 같은 순서로 구현한다.

각각을 조금 더 자세히 설명하면 다음과 같다.
- 환경 변수 지정 : 환경 변수에는 입력 값과 타깃 결괏값이 포함된 데이터셋, 학습률 등이 포함된다. 또한, 활성화 함수와 가중치 등도 선언되어야 한다.
- 신경망 실행 : 초깃값을 입력하여 활성화 함수와 가중치를 거쳐 결괏값이 나오게 한다.
- 결과를 실제 값과 비교 : 오차를 측정한다.
- 역전파 실행 : 출력층과 은닉층의 가중치를 수정한다.
- 결과 출력
오차역전파 심화학습
오차역전파를 이해하기 위해서는 식을 직접 이해해보는 과정이 중요하다.

수치미분으로 가중치와 바이어스를 업데이트 할 시에 많은 시간이 소요된다는 문제점이 있다.
오차역전파의 개념 및 동작원리
- 가중치나 바이어스가 변할 때 마다 최종 오차가 얼마나 변하는지 나타내는 편미분을
- 체인룰(Chain rule)을 이용하여 국소(local)미분으로 분리한 후에
- 이러한 국소 미분을 수학 공식으로 나타내서 계산하는 방법을 오차역전파라고 한다.
* 오차역전파는 수치미분을 사용하지 않고 행렬로 표현되는 수학공식을 계산하기 때문에 빠른 계산이 가능하다.

refernce
N412. 경사하강법과 역전파 알고리즘
🏆 학습목표 경사 하강법(Gradient descent)과 역전파(Backpropagation)에 대해 이해하고 설명할 수 있다. 경사하강법과 역전파 알고리즘을 사용하여 신경망을 구현할 수 있다. 케라스(Keras) 프레임워크를
velog.io
'공부정리 > 모두의 딥러닝 (교재 정리)' 카테고리의 다른 글
| [deeplearning] 모델 설계하기 (1) (0) | 2022.05.16 |
|---|---|
| [deeplearning] 신경망의 이해 - 신경망에서 딥러닝으로 (0) | 2022.05.02 |
| [deeplearning] 신경망의 이해 - 퍼셉트론, 다층 퍼셉트론 (0) | 2022.04.29 |
| [deeplearning] 딥러닝의 동작 원리 - 로지스틱 회귀 (0) | 2022.04.14 |
| [deeplearning] 딥러닝의 동작 원리 - 경사 하강법 (0) | 2022.04.14 |