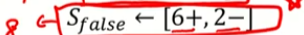이 게시글은 김성범 교수님의 유튜브 강의를 정리한 내용입니다.
내용과 사진의 각 출처는 김성범 교수님께 있음을 미리 알립니다.
해당 게시글 강의 영상: https://www.youtube.com/watch?v=2Rd4AqmLjfU&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=22
[핵심 머신러닝 ] 의사결정나무모델 2 (분류나무, Information Gain)


y는 범주형으로, 비슷한 범주를 가진 것 끼리 묶는 것이 목표

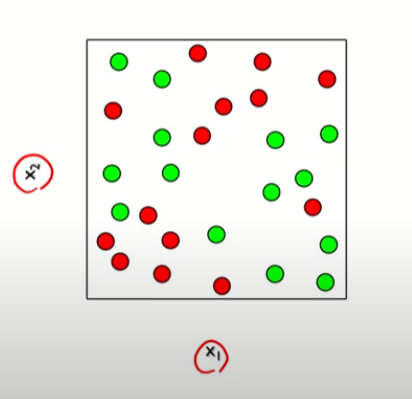
하나의 큰 박스가 점점 나뉘어지는 모습을 볼 수 있다.
분류나무 모델
분류: y가 어떤 연속형 값을 가진 것이 아닌, 범주형 값을 갖고있을 때

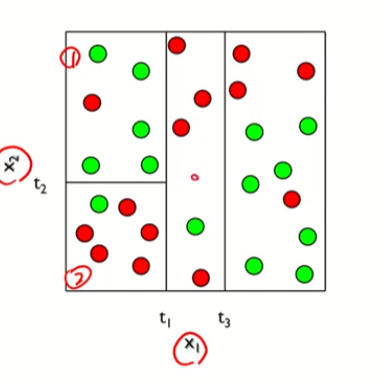
조금 더 나누어보자
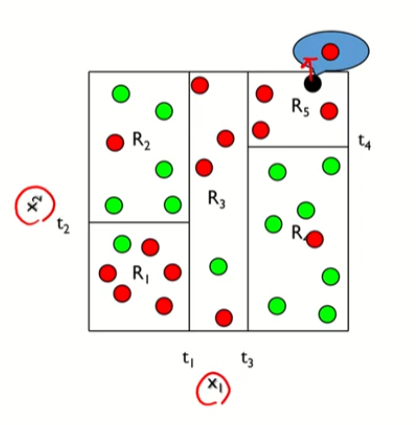
처음보다는 초록색과 빨간색이 꽤 균일하게 나누어진 것을 알 수있다.
 |
 |
그렇다면 새로운 데이터가 들어올 때 해당 값은 해당되는 범주로 예측이 될 것이다.

이 둘은 표현방법은 다르지만 같은 내용이다.

클래스 -> 범주와 같은 이야기이다.
일반적으로 k개의 변수 = k개의 클래스 라고 할 수 있음
p11 => p에서 끝노드 1, 첫번째 범주


여기서argmax를 취한다는 것은 p의 값을 취하는 것임

따라서 0.6의 확률이 속한 클래스를 반환하여 범주예측을 하게된다.

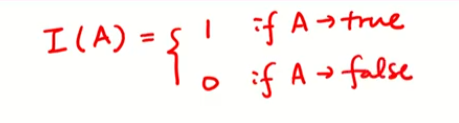

해당되는 것들을 보면 k(3) 항만 남게될 것이다.
해석적인 방법

대부분 2번째 경우로 트리를 보여주는게 많다.
의사결정나무 모델 - 분류모델
분류모델에서의 비용함수 (불순도 측정)
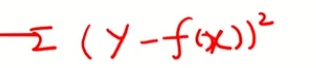
분류모델에서는 좀 다름
크게 세가지가 있다.

1번: 실제 범주와 예상 범주가 잘 매칭되었는지 확인
2번: 지니인덱스
3번 크로스 엔트로피
크로스 엔트로피는 scale 된 엔트로피다. 가운데 p가 1임
x축은 p에 해당하는 것이다.
비용함수 값들이 어떻게 변하는지 나타낸 것


여기서 핵심 포인트는
어떨 때 비용함수가 가장 작아질까? (불순도가 작아질까?)
비용함수를 최소로 하는 j와 s 값을 찾아보자.
1. MisClassification rate을 비용함수로 사용했을 때
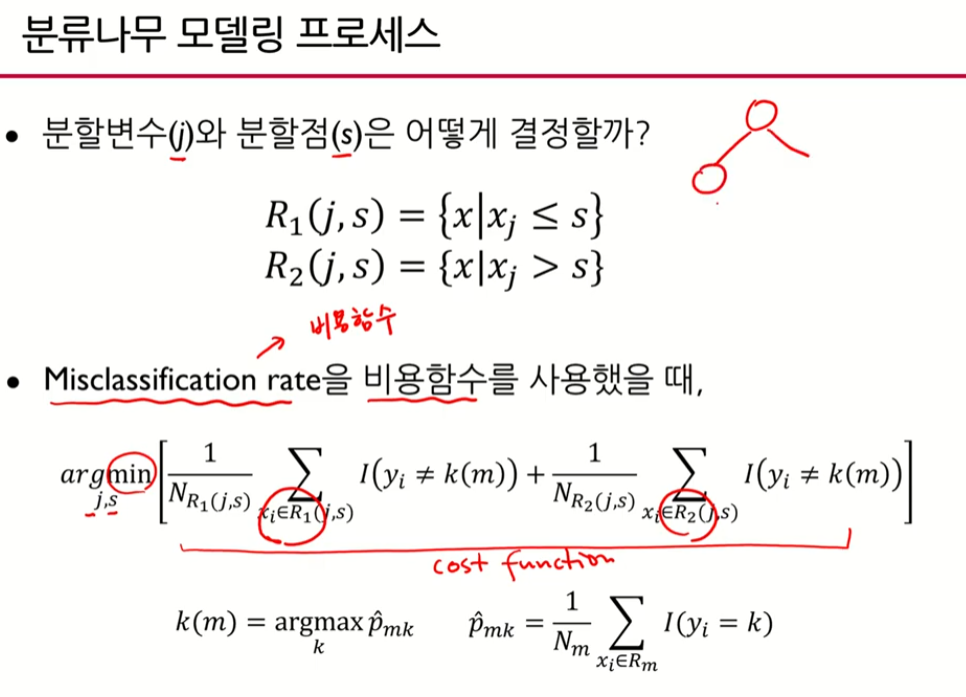
분할법칙

오분류율

2. GINI 지수 계산, Entropy 계산

해당 그림을 보면 불순도가 작을 것이라고 예상됨
클래스는 얼룩말과 하마 두개
지니인덱스는 0~0.5 사이의 값을 가지고있음
엔트로피는 1에 가까울 수록 안좋은 것
information gain - Cross Entropy

엔트로피는 1에 가까울수록 불순도가 높은 것
9+ -> + 클래스가 9개가 있다.
5- -> - 클래스가 5개 있다.
information gain -> 정보를 이용한 것

IG = 전체 데이터에서 특정한 데이터 A를 사용했을 때 엔트로피 감소량
예제
날씨의 조건에 따라서 play를 할 지 말지

informaion gain -> 각 변수에 대한 중요도를 뽑을 수 있음

+ : Y (play) 종속 변수가 yes 인 상태
- : Y (play) 종속 변수가 no인 상태
전체 혼잡도에서 A (wind)라는 변수를 사용했을 때 엔트로피가 얼마나 감소하였는가?
 |

두가지를 계신 해봤을 때 humidity가 감소 폭이 크다.
따라서 wind 보다 humidity가 더 중요함
개별 트리 모델의 단점
개별 트리: 데이터가 있으면 트리를 하나만 만든다. 중간에 error가 발생해도 다음 단계에 에러를 계속 전파해서 누적된다.

나무를 여러개 만들어서 요약하고 최종 결과를 내는 랜덤 포레스트를 이용!
'공부정리 > Deep learnig & Machine learning' 카테고리의 다른 글
| [핵심 머신러닝]뉴럴네트워크모델 1 (구조, 비용함수, 경사하강법) (0) | 2022.08.12 |
|---|---|
| [핵심 머신러닝] 랜덤포레스트 모델 (0) | 2022.08.11 |
| [핵심 머신러닝] 의사결정나무모델 1 (모델개요, 예측나무) - 강의 정리 (0) | 2022.08.11 |
| [머신러닝]Feature Selection (0) | 2022.08.08 |
| [핵심 머신러닝] 정규화모델 2 - LASSO, Elastic Net (0) | 2022.08.08 |