참고 서적
 |
도서명: Deep Learning from Scratch (밑바닥부터 시작하는 딥러닝) 저자 : 사이토 고키 출판 : 한빛 미디어 |
chapter 1 신경망 복습
1.1 수학과 파이썬 복습
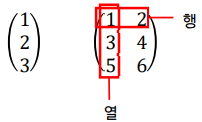
- ‘벡터𝑣𝑒𝑐𝑡𝑜𝑟’와 ‘행렬𝑚𝑎𝑡𝑟𝑖𝑥’
- 벡터 : 크기와 방향을 가진 양. 숫자가 일렬로 늘어선 집합 => 1차원 배열으로 표현 가능
- 행렬 : 숫자가 2차원 형태(사각형 형상)로 늘어선 것\
- 행렬의 원소별𝑒𝑙𝑒𝑚𝑒𝑛𝑡−𝑤𝑖𝑠𝑒 연산
NumPy는 서로 대응하는 원소끼리 (각 원소가 독립적으로) 연산이 이루어지는 element-wise 연산을 지원한다.

- 브로드 캐스트
넘파이의 다차원 배열에서는 형상이 다른 배열끼리도 연산을 지원한다.
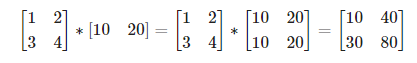

- 벡터의 내적과 행렬의 곱

- x=(x1,…,xn), y=(y1,…,yn) 에 대하여, 백터의 내적은 두 벡터에서 대응하는 원소들의 곱을 모두 더한 것
벡터의 내적은 직관적으로 '두 벡터가 얼마나 같은 방향을 향하고 있는가'를 나타낸다. 벡터의 길이가 1이라고 가정하고, 두 벡터가 완전히 같은 방향이면 두 벡터의 내적은 1이 된다.

np.dot, np.matmul 메서드를 이용해서 행렬 곱을 쉽게 표현 가능하다.
* dot과 matmul의 차이
2차원 행렬곱의 경우 결과가 동일하나 3차원 이상의 행렬끼리 곱할 때 다른 결과를 보여줌
>> import numpy as np
>> A = np.arange(2*3*4).reshape((2,3,4))
>> B = np.arange(2*3*4).reshape((2,4,3))
>> np.dot(A,B).shape
(2, 3, 2, 3)
>> np.matmul(A,B).shape
(2, 3, 3)- np.dot(A,B)의 경우 A의 마지막 축과 B의 뒤에서 두번째 축과의 내적으로 계산_dot product
- (2,3,4) (2,4,3)
- np.matmul(A,B)의 경우 2차원 이상일 시 마지막 2개의 축으로 이루어진 행렬을 나머지 축에 따라 쌓음_matrix product
- (2,3,4) 인 경우 A를 (3*4)행렬을 2개 가지고 있음
내용 참고 및 출처: numpy에서 dot과 matmul의 차이
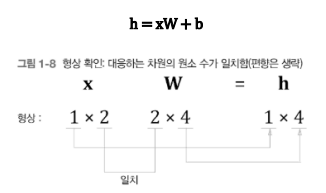
- 행렬 형상 확인

행렬의 곱 등 행렬을 계산할 때는 형상 확인이 중요. 그래야 신경망 구현을 부드럽게 진행할 수 있음
1.2 신경망의 추론
- 신경망 추론의 전체 그림
신경망은 간단히 말하면 단순한 ‘함수’라 할 수 있다. 입력이 들어오면 무엇인가를 출력하는 시스템이다.
=> 신경망도 함수처럼 입력을 출력으로 변환한다.
2차원 데이터를 입력하여 3차원 데이터를 출력하는 함수를 예로 들어보자.
이 함수를 신경망으로 구현하려면 입력층𝒊𝒏𝒑𝒖𝒕 𝒍𝒂𝒚𝒆𝒓에는 뉴런 2개를, 출력층𝒐𝒖𝒕𝒑𝒖𝒕 𝒍𝒂𝒚𝒆𝒓에는 3개를 각각 준비한다. 그리고 은닉층𝒉𝒊𝒅𝒅𝒆𝒏 𝒍𝒂𝒚𝒆𝒓(혹은 중간층)에도 적당한 수의 뉴런을 배치 한다.
- 은닉층에 뉴런이 4개인 경우

np.random.randn() # 표준정규분포 (Standard normal distribution)로부터 샘플링된 난수를 반환
W1 -> 2X4 행렬 형상
입력층 -> 은닉층

은닉층 -> 활성화
* 활성화함수를 통해서 비선형 데이터로 만듦
- 비선형 변환 : 시그모이드 함수(sigmoid function)
- 범위를 0~1사이로 변환함


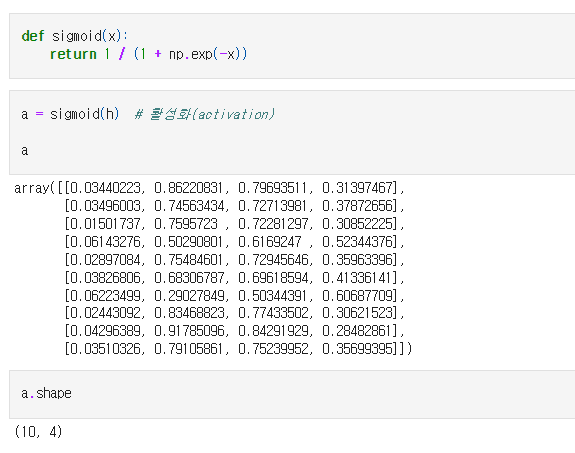
활성화함수를 거친 은닉층 -> 출력층
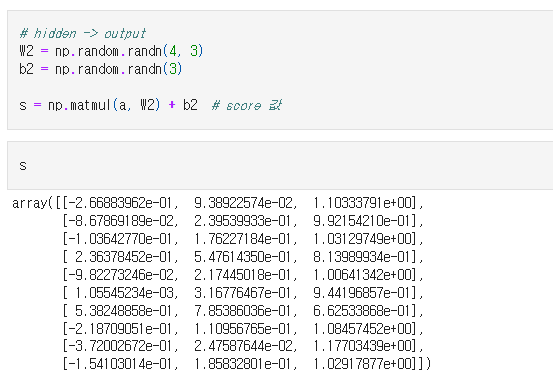
- 계층으로 클래스화 및 순전파 구현
- 완전연결계층(fully connected layer)에 의한 변환은 기하학에서의 아핀(Affine) 변환에 해당
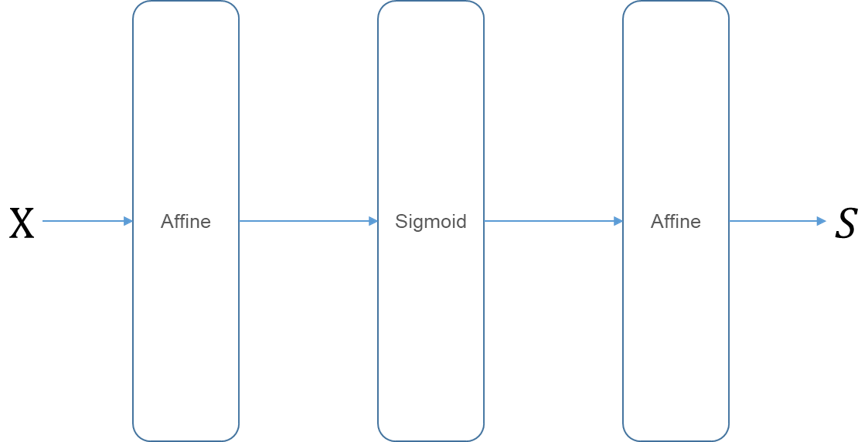
신경망에서 하는 처리를 계층으로 구현해보자. 완전연결계층에 의한 변환을 Affine 계층으로, 시그모이드 함수에 의한 변환을 Sigmoid 계층으로 구현한다. 각 계층은 클래스로 구현하며, 기본 변환을 수행하는 순전파는 forward()로 한다.
• 모든 계층은 forward()와 backward() 메서드를 가진다.
• 모든 계층은 인스턴스 변수인 params와 grads를 가진다. 신경망의 추론 forward()와 backward() 메서드는 각각 순전파와 역전파를 수행한다.
Params는 가중치화 bias 같은 매개변수를 담는 리스트이다.
grads는 params에 저장된 각 매개변수에 대응하여, 해당 매개변수의 gradient(기울기)를 저장하는 리스트이다.

2층 신경망 순전파



- 10x2 형상의 표준정규분포를 따르는 난수 생성
- model 변수에 TwoLayerNet 인자값 입력 (인자값 -> 입력층 크기: 2, 은닉층 크기: 4, 출력층 크기: 3)
- s 변수에 model 변수에서 받은 인자값을 클래스의 predict함수를 통해 순전파 진행
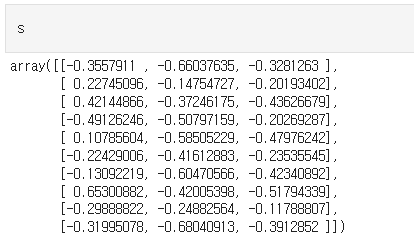
1.3 신경망의 학습
- 손실 함수(Loss Function)
- 신경망의 성능을 나타내는 척도로 손실(loss)을 사용
- 신경망의 손실은 손실 함수를 사용해 구함
- 다중 클래스 분류(multi-class classification)의 경우 교차 엔트로피 오차(CEE, Cross Entropy Error)를 사용
- Softmax 함수의 식은 다음과 같다.
- 즉 class가 n개 일 때, k 번째 클래스의 확률 yk 를 구하는 식

- Cross Entropy 식은 다음과 같다.
- tk는 k번째 클래스에 해당하는 정답 레이블
- log는 밑을 e로 하는 로그
- 정답 레이블 tk는 원-핫 벡터이기 때문에, 실질적으로 1에만 해당하는 인덱스만 계산 된다.

- Softmax with Loss 레이어
- 해당 교재에서는 소프트맥스 함수와 교차 엔트로피 오차를 계산하는 레이어인 SoftmaxWithLoss 클래스를 구현하여 사용한다.
- [밑바닥 부터 시작하는 딥러닝-1]의 5.6.3 에서 확인할 수 있다.
- common/layer.py에서 SoftmaxWithLoss 클래스를 확인할 수 있다.

- 미분과 기울기
예를 들어, L은 스칼라, x는 벡터인 함수
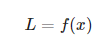
에 대해 벡터의 각 원소에 대한 미분을 계산한 것이 기울기(gradient)이다.
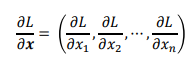
- 연쇄 법칙(Chain Rule)
합성함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.

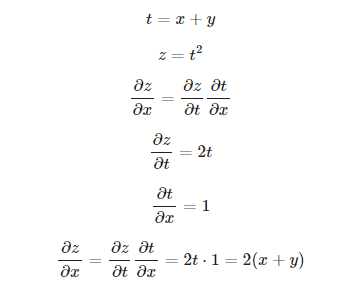
- 계산 그래프
계산 그래프(computational graph)는 계산 과정을 그래프로 나타낸 것이며, 노드(node)와 엣지(edge)로 표현된다. 노드는 연산을 정의하며, 엣지는 데이터가 흘러가는 방향을 나타낸다.
덧셈 노드
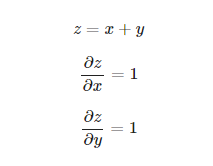
덧셈 노드의 역전파는 입력값을 그대로 흘려보낸다.

곱셈 노드
미분한 값과 각각 x,y값을 교차(??) 로 곱해줌


분기 노드
분기 노드는 선이 두 개로 나뉘면서, 같은 값이 복제(복제 노드라고도 함)된다. 분기노드의 역전파는 상류에서 온 기울기들의 '합'이 된다.
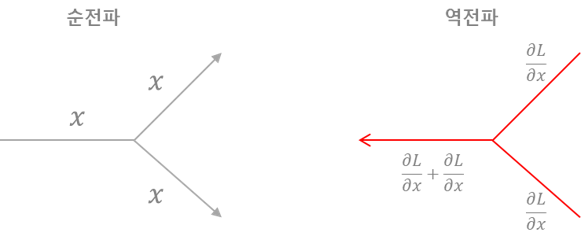
Repeat 노드
분기 노드를 일반화 하면 N개로 분기 되는데, 이를 Repeat 노드라고 한다.



'공부정리 > Deep learnig & Machine learning' 카테고리의 다른 글
| [Deeplearning] 작물 잎 사진으로 질병 분류하기 (2) - Pytorch (0) | 2023.01.10 |
|---|---|
| [Deeplearning] 작물 잎 사진으로 질병 분류하기 (1) 베이스라인 설계- Pytorch (0) | 2023.01.10 |
| [딥러닝] 배치 정규화(Batch Normalization) (0) | 2022.08.29 |
| [딥러닝] 활성화 함수 정리 (0) | 2022.08.22 |
| [딥러닝] 활성화 함수 요약 정리 (0) | 2022.08.22 |