* 이 포스트는 여러 참고 서적과 구글링 내용을 바탕으로 작성하였습니다. 서적 내용의 흐름에 맞게 작성하되, 여러 내용을 보충하여 작성하였습니다.
참고 서적
 |
도서명: Data Science from Scratch (밑바닥부터 시작하는 데이터 과학) 저자 : Joel Grus 출판 : 프로그래밍 인사이트 |
 |
도서명: 인공지능을 위한 수학 저자 : 이시카와 아키히코 출판 : 프리렉 |
ch 4. Linear Algebra
선형대수학(Linear Algebra)는 벡터 공간(Vector space)과 선형 변환(Linear transeformation)을 중심으로 한 학문 체계를 말하며, 다양한 분야에서 폭 넓게 사용하고 있다.
선형대수를 많이 활용하는 이유는 방대한 양의 데이터나 복잡한 시스템을 비교적 간단하게 표현할 수 있을 뿐만 아니라 컴퓨터로도 계산하기 쉽기 때문이다.
4.1.1 Vector
물리학에서 정의되는 벡터의 정의: 크기와 방향으로 정의되는 값
수학에서는 데이터를 한 줄 에 담아낼 수 있게 만든 것으로 부른다고함
- 하나의 문자로 벡터를 표현하는 방법
- 소문자를 굵게 표시 (a,b) // 자주 이용됨
- 문자의 위에 화살표 표시
- 문자에 세로선 장식
- Type of Vector
- 행벡터: 가로로 성분을 나열한 방식
- 열벡터: 세로로 성분을 나열한 방식

4.1.2 덧셈과 뺄셈, 그리고 스칼라 배
- 벡터에는 서로 대응사는 성분끼리 덧셈과 뺄셈을 한다.
- 벡터의 모든 성분에 같은 수를 곱하는 것을 스칼라배라고 한다.
- 서로 다른 차원의 벡터끼리는 덧셈과 뺄셈을 할 수 없다.
차원: 벡터의 성분의 수
- 열벡터의 덧셈과 뺄셈

벡터끼리 덧셈이나 뺄셈을 할 때에는 서로 대응하는 성분끼리 연산한다.
- 스칼라연산

전체 성분에 연산(덧셈, 뺄셈, 곱셈, 나눗셈)을 하면 된다.
스칼라(Scalar): 크기만 있고, 방향이 없는 상수나 변수와 같은 1차원의 값
4.1.3 유향 선분
벡터를 유향선분(화살표)로 가시화하면 이해하기 쉬워짐
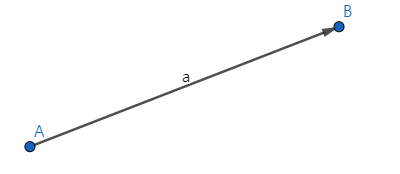
- 단위벡터: 크기가 1인 벡터
- 영벡터(Zero Vector): 크기가 0인 벡터
- 법선 벡터(Normal Vector)
- 벡터 x에 수직(직교)하는 벡터 n
- nx = 0 (법선의 벡터 방정식)

4.1.4 내적
- 내적
- ⟨u,v⟩=u⋅v=u1v1+u2v2+⋯+unvn
- 벡터의 element들끼리 곱한 후 더한다
내적은 연속해서 사용할 수 없다.
4.1.5 벡터의 노름
- 노름(norm)
- 벡터의 이동 거리
- 머신러닝 딥러닝 규제 (regularization) 알고리즘에 사용된다.
- L1 Norm
- 맨해튼 거리
- 벡터 각 성분들의 절댓값을 구한 다음, 모두 더하면 된다.
맨해튼 거리(Manhattan distance, 혹은 택시 거리, L1 거리, 시가지 거리,Taxicab geometry)
19세기 수학자 헤르만 민코프스키가 고안한 용어로, 맨해튼 도시의 건물들이 사각형으로 붙어있는 모습과 닮아서 이름이 붙여짐. 여기서 거리는 Street가 아니라 Distance 이다.

유클리드 기하학의 거리 공간을 좌표에 표시된 두 점 사이의 거리(절댓값)의 차이에 따른 새로운 거리 공간으로 대신하기도 한다. - 위키백과 정의
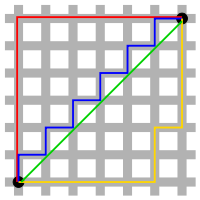
맨해튼 거리와 유클리드 거리의 비교
맨해튼 거리인 빨간색, 파란색, 노란색 선의 길이는 모두 12이며 가장 짧은 맨해튼 거리이다.
유클리드 거리인 초록색 선 (대각선)의 길이는 피타고라스 정리로 계산할 수 있는 값이며, 계산해보면
6 * root(2) 로 가장 짧다.
- L2 Norm
- 유클리드 거리
- 피타고라스 정리와 유사하다.
- n 차원 좌표평면(유클리드 공간)에서 계산 하기 때문에 유클리드 노름(Euclidean norm) 이라고 한다.
유클리드 거리(Euclidean distance)는 두 점 사이의 거리를 계산할 때 흔히 쓰는 방법이다. 이 거리를 사용하여 유클리드 공간을 정의할 수 있으며, 이 거리에 대응하는 노름을 유클리드 노름(Euclidean norm)이라고 부른다. - 위키백과 정의
피타고라스 정리와 유사하지만, 여러차원의 거리를 계산할 수 있다.
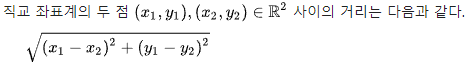
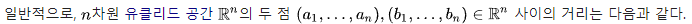

* 코사인 법칙

4.1.6 코사인 유사도
- 코사인 유사도는 -1이상 1 이하의 값을 가진다.
- 두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도이다.

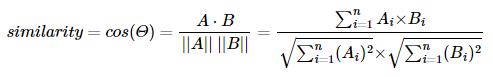
분모 값: 내적
분자 값: L2 노름의 정의 식
- 인공지능이 텍스트를 분석할 때는 내부적으로 단어나 문장을 벡터로 처리한다.
- 벡터로 만들어진 단어나 문장들은 서로의 관계성을 파악할 때 코사인 유사도를 사용한다.
- 코사인 유사도가 높을수록 해당하는 단어나 문장들은 더 가까운 관계이다.
cf. 단어의 벡터화 (Word2Vec)
- Word2Vec
- 단어를 벡터처럼 다루는 방법
- 2013년 구글에서 발표한 논문을 통해 세상에 알려졌다.
다양한 머신러닝 알고리즘과 조합하여 사용되고 있고, 2016년 페이스북에서는 fastText라고 하는 기법이 제안되었다.
https://en.wikipedia.org/wiki/Word2vec
Word2vec - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Models used to produce word embeddings Word2vec is a technique for natural language processing published in 2013. The word2vec algorithm uses a neural network model to learn word assoc
en.wikipedia.org
- fastText
- Word2Vec의 연장선상에서 언어를 벡터로 표현하는 방법.
https://en.wikipedia.org/wiki/FastText
fastText - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search fastText is a library for learning of word embeddings and text classification created by Facebook's AI Research (FAIR) lab.[3][4][5][6] The model allows one to create an unsupervised l
en.wikipedia.org
Reference