참고 서적
 |
도서명: Data Science from Scratch (밑바닥부터 시작하는 데이터 과학) 저자 : Joel Grus 출판 : 프로그래밍 인사이트 |
Ch 4. 선형대수
4.1 거리 유사도 측정방법
Euclidean Distance
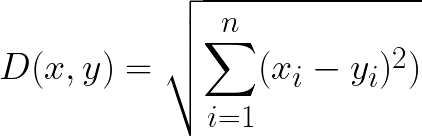
- 두 점 p, q사이의 유클리디안 거리를 구하면 이 두 점의 최단거리가 된다.
- 다음 코드는 넘파이 라이브러리를 활용하여 두 점 사이의 유클리디안 거리를 이용한 코드이다.
- 두 가지 개체의 속성값들이 여러개 일 경우 이들 속성값들에 의한 두 개체 사이의 유사도를 구할 때 자주 사용함
import numpy as np
point1 = np.array((1, 1))
point2 = np.array((2, 2))
dist = np.linalg.norm(point1 - point2)
print(dist) # 1.41421
2. Cosine Similarity

- 코사인 유사도는 내적공간의 두 벡터간 각도와 코사인값을 이용하여 측정된 벡터간 유사한 정도이다. 코사인 유사도는 '방향'에 대한 유사도이다. 즉, '거리'는 고려하지 않는다는 거다.
- 여기서 유클리디안 거리와 코사인 유사도의 차이점이 드러난다. 거리 기반 (ex.유클리디안 거리)은 좌표를 기준으로, 가까운 좌표에 있는 점들이 유사도가 높다고 측정되는 반면, 각도 기반 (ex.코사인 유사도)은 기울기와 방향이 같은 벡터가 유사도가 높다고 측정된다.
- 코사인 유사도는 2차원보다 높은 차원의 데이터, 또 벡터의 크기가 중요하지 않은 데이터에 주로 사용된다.

출처 : http://school.fastcampus.co.kr/blog/data_dss/60/
3. Hamming Distance
- 두 문장 간 편집거리를 측정하기 위한 문자열 메트릭으로, 같은 길이를 가진 2개의 문자열(a, b)을 a에서 b로 바꾸기 위해 몇 개의 글자를 바꿔줘야하는지에 대한 거리이다.
- 해밍거리의 가장 큰 단점은 비교하고자 하는 두 문자의 거리가 같아야한다는 점이다.
- 두 문자의 해밍거리 계산을 위해 XOR 연산을 수행한 후 나온 값에서 1의 개수를 세면 거리가 된다.
- 예를 들어 1101과 1111이라는 문자열이 있다고 가정하자. XOR 연산을 수행하면
- 1101 ⊕ 1111 = 0010 이므로, 해밍거리 d ( 1101, 1111 ) = 1 이다.
4. Manhattan Distance

- 맨하탄 거리는 두 점 p, q가 있을 때, 가상 체스보드가 있다고 생각하고 오직 수평, 수직 이동만 하여 p에서 q까지 이동할 때 최단으로 걸리는 거리이다.
5. Chebyshev Distance
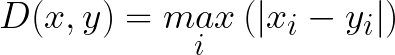
- 두 점 p, q간 좌표 차원을 따라 가장 긴 거리를 거리값으로 선택하는 방식이다.
- 식에서도 볼 수 있다시피 max(p, q)라고 써있다. (가장 긴 거리를 사용)
- 유클리디안이나 맨하탄에 비해 사용하는 케이스가 매우 한정적이다.
- 예를 들어, 최소한의 움직임 횟수를 도출하고자 할때 용이할 수 있다. (예를 들어, 4번만 방향을 꺾어서 목표지점에 도달해야하는 경우?)
6. Minkowski Distance
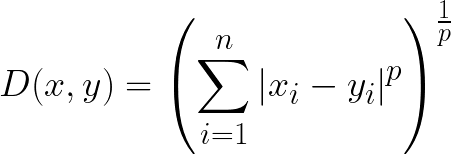
- 민코프스키 거리는 유클리디안 거리와 맨해튼 거리를 일반화한 거리 공식이다.
7. Jaccard Index


- 자카드 인덱스는 두 문장을 각각 단어의 집합으로 만든 뒤, 두 집합의 교집합과 합집합을 활용하여 유사도를 측정하는 방법이다.
- 아래의 그림을 예로 들어보자. 컴퓨터가 예측한 스탑사인은 빨간색 박스이고, 실제 스탑사인은 초록 박스이다. 이때, 자카드 인덱스는 두 박스가 겹치는 부분이 많을수록 그 값이 커지게 된다.

8. Haversine

- 하버사인 거리는 두 점 p, q의 거리를 구할 때 지구의 곡률을 고려하여 거리를 구하게 된다.
- 컴퓨터 자료상 거리가 아닌, 실제 서울-부산의 거리를 구할 때는 단순히 직선거리로 거리를 구해선 안된다. 왜냐하면 지구가 둥근 특성 때문에 곡률이 발생하기 때문이다.
- 그렇기 때문에 만약 지리정보에 관련된 좌표를 다룬다면, 거리를 구할 때 이를 고려해야 한다.
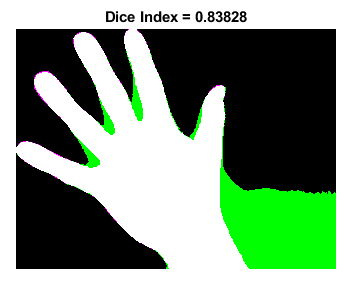
9. Sørensen-Dice Index

- Jaccard Index와 유사한 방식으로 계산이 보다 직관적이고 F1 Score와 유사한 형태로 계산을 한다.
- 영상 분할에 주로 쓰인다. (image segmentation)
- 이미지등의 Segmentation 에서 쓰이는 지표
- 영상 이미지등에서 정답과 예측값간의 차이를 알기위해 쓴다.
- 무슨 축약된 단어는 아니고 사람이름이다. Sørensen–Dice coefficient 라고도 하며, F1 Score와 개념상 같지만, 영상처리에서 더 강조를 하는 경향이 있다.
- 라벨링된 영역과 예측한 영역이 정확히 같다면, 1이되며 그렇지 않을 경우에는 0이 된다.
- F1은 알다시피, 리콜과 정밀도의 조화평균이다. 즉, 두개다 동시에 고려하는 조화로운 지표라는 것이다.

출처: 9 Distance Measures in Data Science (by Maarten Grootendorst)
유클리디언 거리 vs 마할라노비스 거리 비교
다음과 같은 데이터 분포가 있다고 하자. 일반적인 거리(=유클리디언 거리)로 보면 X는 B보다 A에 가깝다.

그림1
하지만 데이터의 퍼진 모양을 보면 XB방향에 평행하게 길게 늘어져있음을 볼 수 있다. XA방향으로도 퍼져있지만 XB방향보다는 덜 퍼져있다. 이러한 분산을 적용하여 거리를 재계산하면 다음과 같은 축을 그려볼 수 있게된다.
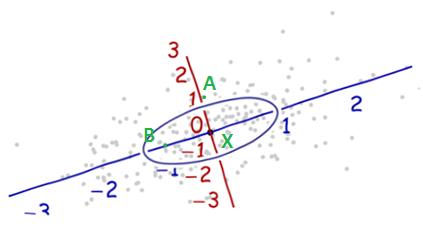
그림2
즉 A방향으로는 좁은 범위의 분포를 이루고, B방향으로는 넓은 분포를 이루기때문에, 각 분포의 크기에 대한 상대적인 거리를 보면 B는 X에 무척 가까운 값으로 해석할 수 있다. 이것이 마할라노비스 거리의 특징이다.
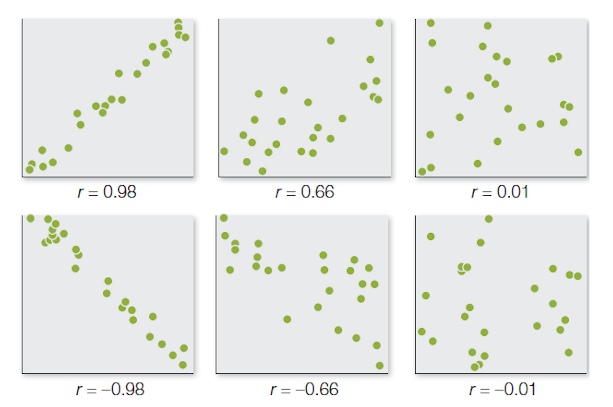
10. 피어슨 상관계수(Pearson correlation coefficient)
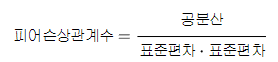

- 피어슨 상관계수는 위와 같은 공식을 사용한다. 공분산에 표준편차를 이용하여 정규화를 진행한 것으로 다양한 머신러닝 분야에서 활용이 가능하다.
- 피어슨 상관계수를 활용한 대표적인 기법으로는 사람간의 유사도를 측정하는 추천 시스템(ex: Collaborative Filtering)이 대표적이다.
- 추천 시스템의 상징이라 할 수 있는 협업 필터링에서 가장 많이 활용되는 사람간의 유사도 측정 방식에 피어슨 상관계수를 많이 활용하기 때문이다.
- 상관계수가 높을수록 두 값은 서로 연관이 있다는 뜻이기 때문에 유사도 측정에 많이 활용이 되어서 평점 시스템이 있는 컨텐츠의 유사도 측정으로 많이 활용된다. 그래서 피어슨 상관계수를 활용하여 피어슨 유사도라는 말로도 불리고 있다.
Reference
Ch 5. 통계
분산
하나의 변수가 변수의 평균에서 얼마나 멀리 떨어져 있는지 계산
공분산
두 변수가 각각의 평균에서 얼마나 멀리 떨어져 있는지
심슨의 역설
혼재변수(confounding variables)가 누락되어 상관관계가 잘못 계산되는 심슨의 역설(simp son’s paradox)을 흔히 직면하게 된다.
예) 미국 서부, 동부 과학자 친구수 (석사, 박사에 따라 수가 다르고…)
베이즈 정리
조건부 확률을 반대로 뒤집는 ‘베이즈 정리’
(조건부확률 ) 사건 E가 발생했다는 가정하에, 사건 F가 발생할 확률만 주어졌을때,
(베이즈 정리) 사건 F가 발생했다는 가정하에, 사건 E가 발생할 확률은?
P(E|F) = P(E,F)/P(F) = P(F|E)P(E)/P(F)
사건 F = 사건F와 사건 E가 모두 발생하는 경우 + 사건 F는 발생하지만 사건 E는 발생하지 않는 경우
P(F) = P(F,E) + P(F,^E)
베이즈정리 = P(E|F) = P(F|E)P(E) / [P(F|E)P(E) + P(F|^E)P(^E)]
확률변수
확률변수(random variable) 특정 확률분포와 연관되어 있는 변수
모델
가장 적합한(best) 모델이란? 모델의 오류(error)를 최소화하는 또는 likelihood(우도)를 최대화 하는 것을 의미한다.
출처: https://ourcstory.tistory.com/222 [불로:티스토리]
Ch 6. 확률
독립사건과 종속사건
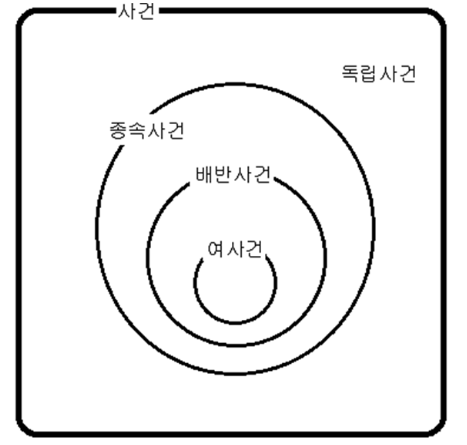


독립사건: 서로 영향을 끼치지 않음
배반사건: 같이 일어날 일이 절대 없음 (같이 일어나지 말아야한다는 것은 서로 영향을 준다는 것..)
중심극한정리
Reference
독립변수(獨立變數, independent variable)와 종속변수(從屬變數, dependent variable)는 실험으로 획득한 데이터를 통해 수학적 모델을 세우거나 통계적 모델을 세울 때 사용되는 변수의 두 종류다. 종속변수가 독립변수에 의해 영향을 받는다고, 즉 종속되어있다고 해석하기 때문에 이러한 이름이 붙여졌다. 따라서 독립변수는 입력값이나 원인을 나타내며, 종속변수는 결과물이나 효과를 나타낸다. 기타 여러 가지 원인으로 관찰 중인 변수들은 기타 변수라고 한다
'공부정리 > Data Science' 카테고리의 다른 글
| [Data Science from Scratch] Chapter 11. machine learning (0) | 2022.07.21 |
|---|---|
| [Data Science from Scratch] ch.7, 8 additional note - Gradient Descent without FrameWork! (0) | 2022.07.20 |
| [Data Science from Scratch] ch 4. Linear Algebra - (1) Vector (0) | 2022.07.07 |
| [Data Science from Scratch] Chepter 1,2,3 Additional note (0) | 2022.07.01 |
| [Data Science from Scratch] Ch 3. Visualizing Data (0) | 2022.06.30 |