참고 서적
 |
도서명: 모두의 딥러닝 저자 : 조태호 출판 : 길벗 발매 : 2020.01.27 |
딥러닝을 위한 기초 수학
꼭 알아야하는 토픽과 간단한 소개만 하고 넘어가겠습니다.
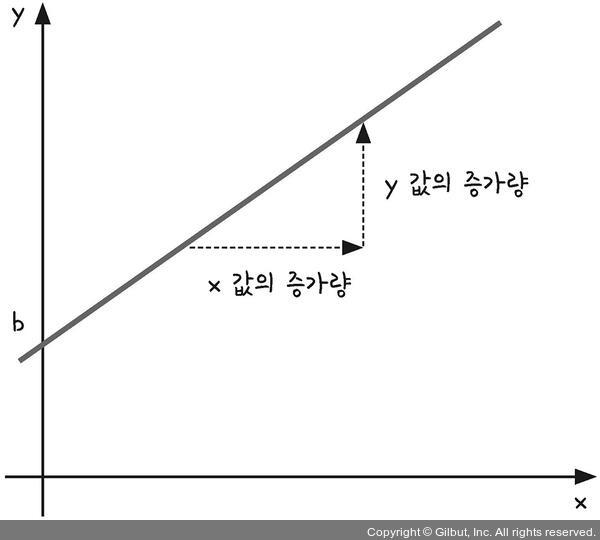
1. 일차 함수, 기울기와 y 절편
y = ax+b (a !=0)인 일차함수 식에서 x가 주어지고 원하는 y값이 있을 때, 적절한 a와 b 값을 찾는 것을 딥러닝의 과정으로 볼 수 있습니다.
2. 이차 함수와 최솟값
y = ax^2 (a != 0)은 포물선을 그리는 그래프로, 포물선의 최저점이 최솟값이 됩니다. 딥러닝을 실행할 때 이 최솟값을 찾아내는 것이 중요합니다. 이때 최솟값은 '최소 제곱법'으로 구할 수 있습니다.

3. 미분, 순간 변화율과 기울기
최소 제곱법을 사용하기에 충분한 조건이 없을 때 미분을 이용합니다. 이차 함수의 최솟값은 미분을 통해 구할 수 있기 때문입니다.

4. 편미분
그냥 미분과 달리 편미분은 식에 여러 가지 변수가 있을 때, 딱 하나의 변수에 대해서만 미분하고 나머지는 상수로 취급하여 미분하는 것입니다.
미분과 더불어 딥러닝을 공부할 때 가장 자주 접하게 되는 또 다른 수학 개념은 바로 편미분입니다. 미분과 편미분 모두 ‘미분하라’는 의미에서는 다를 바가 없습니다. 그러나 여러 가지 변수가 식 안에 있을 때, 모든 변수를 미분하는 것이 아니라 우리가 원하는 한 가지 변수만 미분하고 그 외에는 모두 상수로 취급하는 것이 바로 편미분입니다. 예를 들어 f(x) = x과 같은 식을 미분할 때는 변수가 x 하나뿐이어서 미분하라는 의미에 혼란이 없습니다. 그러나 다음 식을 보겠습니다.
f(x, y) = x2 + yx + a (a는 상수)
여기에는 변수가 x와 y, 이렇게 두 개가 있습니다. 그러면 이 중 어떤 변수로 미분해야 하는지를 정해야 하므로 편미분을 사용하는 것입니다. 만일 이 식처럼 여러 변수 중에서 x에 관해서만 미분하고 싶다면, 함수 f 를 ‘x에 관해 편미분하라’고 하며 다음과 같이 식을 씁니다.
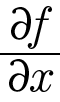
그러면 앞에 나온 함수 f(x, y) = x2 + yx + a를 x에 관해 편미분 하는 과정은 어떻게 될까요? 먼저 바로 앞에서 배운 미분의 성질 4번에 따라 x2항은 2x가 됩니다. 그리고 x에 관해 미분하면 다른 모든 항은 상수로 취급하므로 y는 상수가 됩니다. 따라서 미분의 성질 3번에 따라 xy는 y가 됩니다. 마지막 항 a는 미분의 성질 1번에 따라 0이 됩니다. 이를 정리하면 다음과 같이 나타낼 수 있습니다.
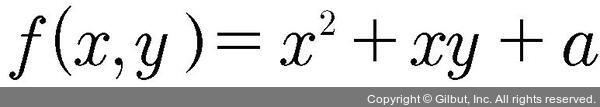
일 때,
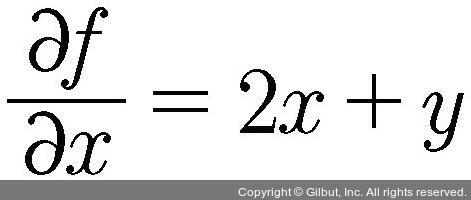
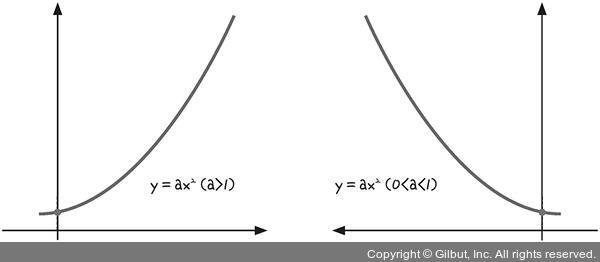
5. 지수와 지수 함수
지수
변수 x가 지수 자리에 있는 경우를 말합니다.
6. 시그모이드 함수
시그모이드 함수라는 이름이 생소할 수 있습니다. 시그모이드 함수는 분모에 있는 지수 함수의 밑이 자연 상수 e인 함수입니다. 식으로 표현하면 f(x) = 1/(1+e^(-x))입니다. 그래프로 표현하면 아래와 같습니다.


x가 큰 값을 가지면 f(x)는 1에 가까워지고, x가 작은 값을 가지면 f(x)는 0에 가까워집니다. S자 형태로 그려지는 이 함수의 속성은 0 또는 1, 두 개의 값 중 하나를 고를 때 유용하게 쓰입니다.
딥러닝을 배우는 우리에게 지수 함수가 중요한 이유는 지금 배울 시그모이드 함수를 이해해야 하기 때문입니다. 시그모이드 함수는 지수 함수에서 밑의 값이 자연 상수 e인 함수를 말합니다. 자연 상수 e는 ‘자연 로그의 밑’, ‘오일러의 수’ 등 여러 이름으로 불리는데, 파이(π)처럼 수학에서 중요하게 사용되는 무리수이며, 그 값은 대략 2.718281828…입니다.
자연 상수 e가 지수 함수에 포함되어 분모에 들어가면 시그모이드 함수가 되는데, 이를 식으로 나타내면 다음과 같습니다.
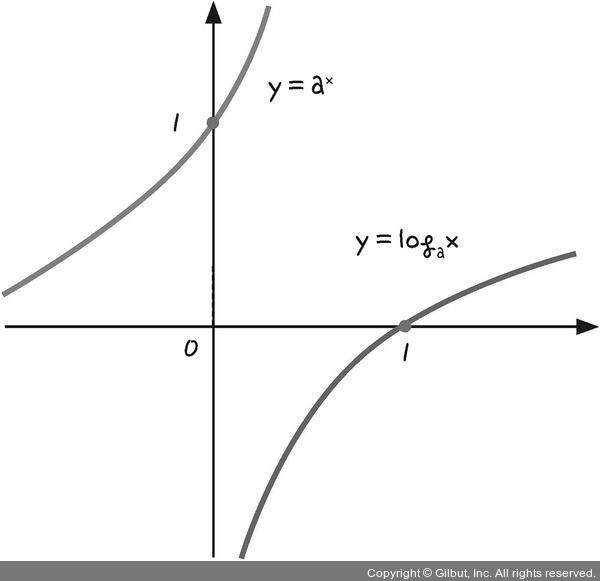
7. 로그와 로그 함수

로그함수는 지수의 역함수입니다. 역함수는 x와 y를 서로 바꾸어 가지는 함수입니다.
지수 함수 y = ax(a ≠ 1, a > 0)는 로그의 정의를 따라 x = loga y로 바꿀 수 있습니다.
'공부정리 > 모두의 딥러닝 (교재 정리)' 카테고리의 다른 글
| [deeplearning] 신경망의 이해 - 오차 역전파 (0) | 2022.04.29 |
|---|---|
| [deeplearning] 신경망의 이해 - 퍼셉트론, 다층 퍼셉트론 (0) | 2022.04.29 |
| [deeplearning] 딥러닝의 동작 원리 - 로지스틱 회귀 (0) | 2022.04.14 |
| [deeplearning] 딥러닝의 동작 원리 - 경사 하강법 (0) | 2022.04.14 |
| [deeplearning] 딥러닝의 동작 원리 - 선형 회귀 (0) | 2022.04.14 |