문제 해결이란?
초기 상태에서 목표상태에 도달하는 과정이다.
8-Puzzle
타일을 1부터 8까지 순서대로 배치하는 게임

• 상태(state): Location of tiles: 8개의 타일의 각각의 위치와 빈칸의 위치
• 동작(action): Move blank Left, Right, up, down: 빈칸으로 왼쪽, 오른쪽, 위, 아래 이동
• 목표 도달 확인(goal test): 주어진 목표상태에 도달하였는지 확인
• 경로 비용(path cost): 한번 action할 때마다 1씩 증가 (경로의 수)
상태공간 그래프
인공지능에서는 최적의 해를 찾기 위해, 각 동작에 따른 상태 변화를 그래프로 나타내어 해결한다.

이러한 문제 해결과정에 있어서 우리는 다음과 같은 탐색 방법을 찾아볼 수 있다.
그래프 탐색 알고리즘 DFS & BFS
- 탐색(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정이다.
- 대표적인 그래프 탐색 알고리즘으로는 DFS와 BFS가 있다.
오늘 포스팅할 주제로는 8-Puzzle의 BFS, DFS 구현을 다뤄보도록 하겠다.
8-Puzzle의 기본적 구성
먼저 8-Puzzle의 기본적 구성에 대하여 설명하겠다.

1) 보드를 어떻게 표현할 것인가?
이 부분에 대한 설명은 오하영 교수님의 유튜브에서 친절하게 설명하고 있으니 참고하길 바란다.
파이썬의 클래스를 이용하여 하나의 상태(state)를 나타낸다.

클래스 안의 1차원 리스트 board를 이용하여 8-puzzle의 보드를 표현한다.
예를들어 시작노드는 아래와 같이 생성할 수 있다. (보드에 있는 빈칸은 0으로 나타낸다)

2) Open Close 리스트
탐색에서는 중복된 상태를 막기 위하여 다음과 같은 2개의 리스트를 사용한다.
- OPEN 리스트: 확장은 되었으나 아직 탐색하지 않은 상태들이 들어 있는 리스트
- CLOSED 리스트: 탐색이 끝난 상태들이 들어 있는 리스트
open과 closed 리스트는 파이썬의 리스트를 이용하여 구현된다. 리스트에서 첫번째 요소를 가져오려면 pop(0) 함수를 사용한다. 리스트의 끝에 값을 추가하려면 append() 함수를 이용한다. 리스트의 처음에 값을 추가하려면 insert(0,s) 함수를 사용한다.

3) 자식노드들은 어떻게 생성할 것인가?
자식 노들들은 빈칸을 상하좌우로 움직여서 생성할 수 있다. 빈칸은 숫자 0으로 표현되므로 index()함수를 이용하여 리스트에서 0을 찾아서 인덱스 값으로 어떤 연산자가 가능한지 판단한다. 가능한 연산자가 발견되면 연산자를 적용하여 결과 리스트에 새로운 상태로 추가한다.

보드를 구성하는 전체 소스 코드
# 상태를 나타내는 클래스
class State:
def __init__(self, board, goal, moves=0):
self.board = board
self.moves = moves
self.goal = goal
# i1과 i2를 교환하여서 새로운 상태를 반환한다.
def get_new_board(self, i1, i2, moves):
new_board = self.board[:]
new_board[i1], new_board[i2] = new_board[i2], new_board[i1]
return State(new_board, self.goal, moves)
def expand(self, moves):
result = []
i = self.board.index(0) # 숫자 0(빈칸)의 위치를 찾는다.
if not i in [0, 1, 2]: # UP 연산자
result.append(self.get_new_board(i, i - 3, moves))
if not i in [0, 3, 6]: # LEFT 연산자
result.append(self.get_new_board(i, i - 1, moves))
if not i in [2, 5, 8]: # DOWN 연산자
result.append(self.get_new_board(i, i + 1, moves))
if not i in [6, 7, 8]: # RIGHT 연산자
result.append(self.get_new_board(i, i + 3, moves))
return result
# 객체를 출력할 때 사용한다.
def __str__(self):
return str(self.board[:3]) + "\n" + \
str(self.board[3:6]) + "\n" + \
str(self.board[6:]) + "\n" + \
"------------------"
def __eq__(self, other):
return self.board == other.board이제, 보드의 클래스를 구성하였으면 BFS를 구현해보도록 하자.
8-Puzzle BFS

BFS는 Queue를 이용하여 탐색을 하는데,
while 문의 반복으로 통하여 open_queue에 아무것도 남아있지 않을 때 까지 반복한다.
8-Puzzle의 open_queue에는 8Puzzle이 이동한 상태공간들이 들어있다.
open_queue에 append 순차적으로 들어가서 탐색된 상태들은 방문처리를 해준다.
방문처리는 closed_queue 에 넣어준다.
이 과정을 반복하면서
일단, BFS의 기본적인 자료구조는 FIFO (선입 선출)이다.
목표상태에 도달하지 않았고, open_queue와 closed_queue에 남아있으면 먼저온 순서대로 pop해준다.
pop(0) -> 첫번 째 들어 있는 값을 지워준다.
이 과정을 반복하면서 상태공간을 탐색한다. 만약 open_queue와 closed_queue에 없다면 if 조건문을 통하여
새로운 상태공간을 open_queue에 넣어준다.
# open 리스트
open_queue = [ ]
open_queue.append(State(puzzle, goal))
closed_queue = [ ]
moves = 0
while len(open_queue) != 0:
current = open_queue.pop(0)# OPEN 리스트의 앞에서 삭제
print(current)
if current.board == goal:
print("탐색 성공")
break
moves = current.moves+1
closed_queue.append(current)
for state in current.expand(moves):
if (state in closed_queue) or (state in open_queue): # 이미 거쳐간 노드이면
continue # 노드를 버린다.
else:
open_queue.append(state)# OPEN 리스트의 끝에 추가
전체 소스코드는 github에 올려두었다.
GitHub - Kangsuyeon01/Capstone-design1_AI-Project
Contribute to Kangsuyeon01/Capstone-design1_AI-Project development by creating an account on GitHub.
github.com
출력 결과


이러한 8-Puzzle 의 상태공간에 대하여 아래와 같은 트리구조를 그릴 수 있다.
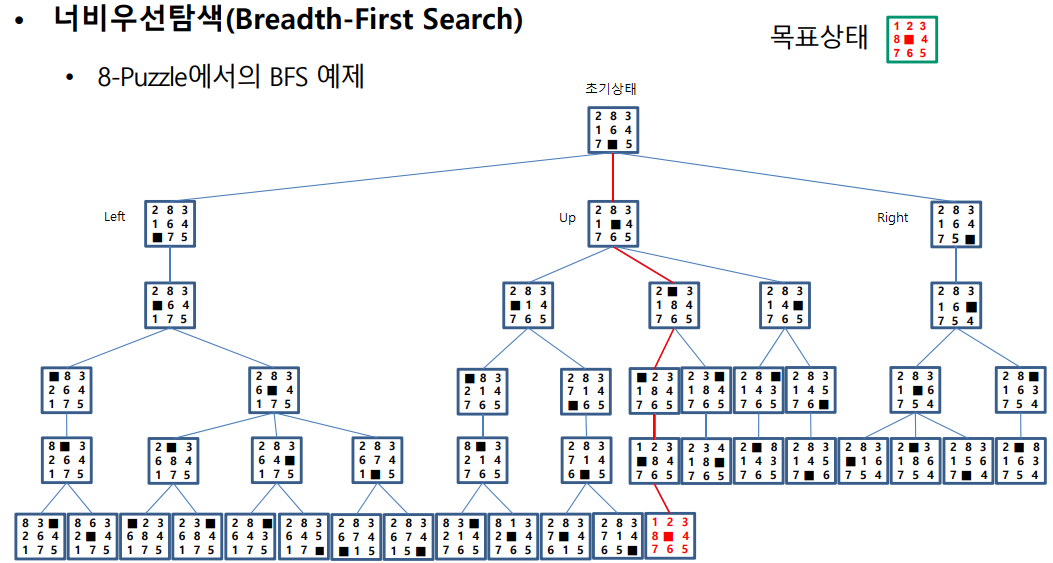
내 코드는 클래스를 구성함에 있어, UP연산자가 가장 먼저 실행되기 때문에 UP으로 먼저 BFS 상태공간을 탐색하는 것이다. 따라서, Left 연산자가 먼저 실행된 위의 그림과 내 코드의 트리구조 순서가 다를 수 있다.
8-Puzzle DFS

DFS는 Stack을 이용하여 탐색을 하는데,
while 문의 반복으로 통하여 open_stack에 아무것도 남아있지 않을 때 까지 반복한다.
8-Puzzle의 open_stack에는 8Puzzle이 이동한 상태공간들이 들어있다.
open_stack에 append 순차적으로 들어가서 탐색된 상태들은 방문처리를 해준다.
방문처리는 closed_stack 에 넣어준다.
일단, DFS의 기본적인 자료구조는 LIFO (선입 후출)이다. 즉, 먼저 들어온 상태공간은 제일 나중에 나간다는 것이다.
그리고, 구현에 있어서 백트래킹이 가장 중요하다. DFS 로 깊이를 탐색하고, 만약 목표상태에 도달하지 못하였으면 그 전의 상태로 돌아가 다른 곳을 탐색해야하기 때문이다.
목표상태에 도달하지 않았고, open_stack과 closed_stack에 남아있으면 마지막에 있는 상태공간을 pop()해준다.
pop() -> 마지막에 있는 값을 지워준다.
이 과정을 반복하면서 상태공간을 탐색한다. 만약 open_stack과 closed_stack에 없다면 if 조건문을 통하여
새로운 상태공간을 open_stack에 넣어준다.
이 부분을 구현하기위해 연구실 사람들과 머리를 맞대어 보았다..
# open 리스트
open_stack = [ ]
open_stack.append(State(puzzle, goal))
closed_stack = [ ]
moves = 0
cnt = 0
while len(open_stack) != 0:
current = open_stack[len(open_stack) - 1]
cnt += 1
print("탐색 횟수:",cnt)
print(current)
if current.board == goal:
print('탐색 성공')
break
moves = current.moves + 1
tmp = True
for state in current.expand(moves): #current에서 move 나올 수 있는 상태공간에 관한 for문
tmp = True
if (state not in open_stack) and (state not in closed_stack) : #만약 open_stack과 colsed_stack 안에 없으면
open_stack.append(state) #open_stack 안에 추가해준다.
tmp = False
break
if tmp == True: #만약 for 문의 if문을 통과하지 못한 상태로 남으면 tmp가 ture 로있을 것이다.
open_stack.pop() #open_stack을 pop한다. (back tracking)
closed_stack.append(current) #현재 노드를 방문 처리(closed_stack 에 추가)
else:
print('탐색 실패')출력결과

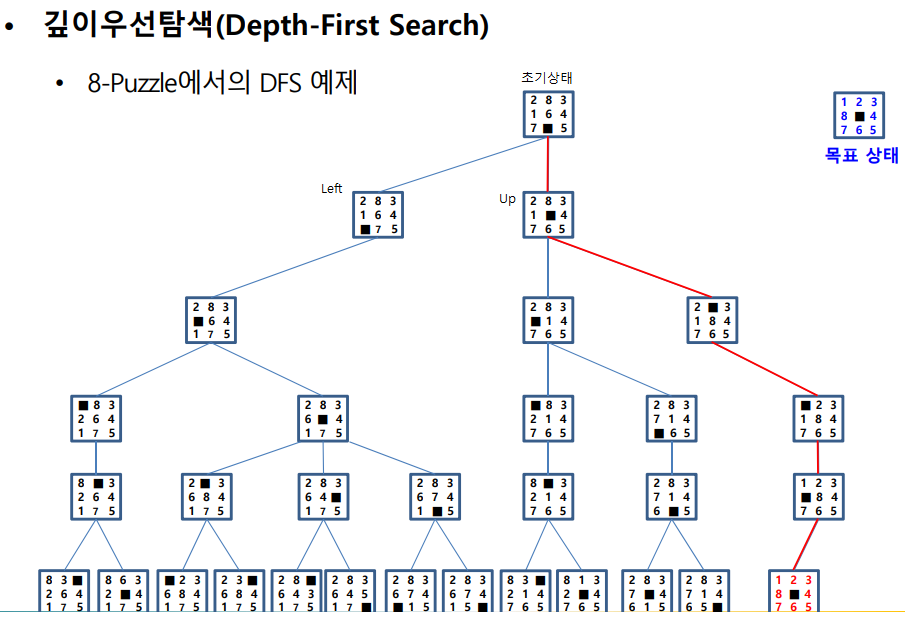
내 코드는 클래스를 구성함에 있어, UP연산자가 가장 먼저 실행되기 때문에 UP으로 먼저 DFS 상태공간을 탐색하는 것이다. 따라서, Left 연산자가 먼저 실행된 위의 그림과 내 코드의 트리구조 순서가 다를 수 있다.
전체 소스코드는 github에 올려두었다.
GitHub - Kangsuyeon01/Capstone-design1_AI-Project
Contribute to Kangsuyeon01/Capstone-design1_AI-Project development by creating an account on GitHub.
github.com
아직 미흡한 점이 많을 수 있습니다. 댓글을 통해서 틀린 점이나 수정해야할 사항들을 남겨주시면 차차 개선해나가겠습니다. 감사합니다 :)
[알고리즘] 그래프 탐색 알고리즘 : DFS & BFS (2) / Python
그래프 탐색 알고리즘 DFS & BFS 탐욕(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정이다. 대표적인 그래프 탐색 알고리즘으로는 DFS와 BFS가 있다. * 코딩테스트에서 자주 등장하
sillon-coding.tistory.com
[알고리즘] 그래프 탐색 알고리즘: DFS & BFS (1) / Python
그래프 탐색 알고리즘 DFS & BFS 탐욕(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정이다. 대표적인 그래프 탐색 알고리즘으로는 DFS와 BFS가 있다. * 코딩테스트에서 자주 등장하는
sillon-coding.tistory.com
'python > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 스택, 큐, 재귀함수 / Python 파이썬 (0) | 2022.05.06 |
|---|---|
| [알고리즘] 정렬 알고리즘 / Python 파이썬 (0) | 2022.05.03 |
| [자료구조] 해시, 해시법(hashing) / Python 파이썬 (0) | 2022.04.12 |
| [자료구조] 검색 알고리즘 (선형 검색/ 이진 검색) / Python 파이썬 (0) | 2022.04.12 |
| [알고리즘] 그래프 탐색 알고리즘 : DFS & BFS / Python 파이썬 (0) | 2022.04.05 |