정렬이란?
섞여 있는 데이터를 순서대로 나열하는 것
정렬 알고리즘은 시간 복잡도에 따라 성능을 좌우되며 성능이 좋을수록 구현 방법이 어려워진다.
대표적인 정렬의 종류
O(n²)의 시간 복잡도 (정렬할 자료의 수가 늘어나면 제곱에 비례해서 증가)
- 버블 정렬(Bubble Sort)
- 선택 정렬(Selection Sort)
- 삽입 정렬(Insertion Sort)
O(n log n)의 시간 복잡도
- 병합 정렬(Merge Sort)
- 퀵 정렬(Quick Sort)
1. 거품 정렬 (Bubble Sort)
정렬 중에서도 가장 직관적인 정렬 방식이다.
거품 정렬은 인접한 두 수를 비교하고, 가장 큰 값을 뒤로 보낸다. 알고리즘 동작이 각 순회의 가장 큰 요소가 맨 뒤로 이동(Bubble Up) 하는 방식이기 때문에 지어진 이름이다.
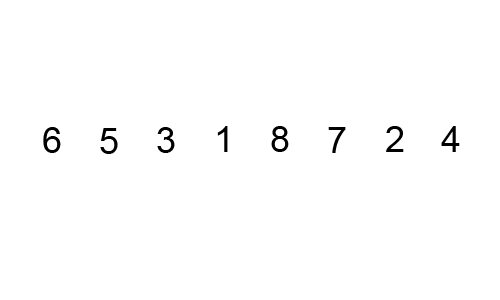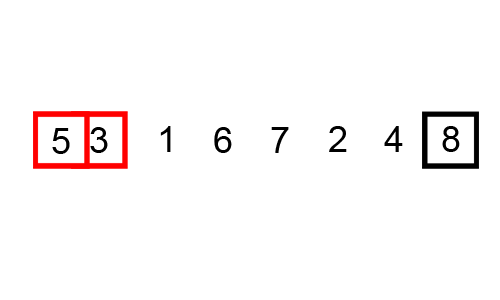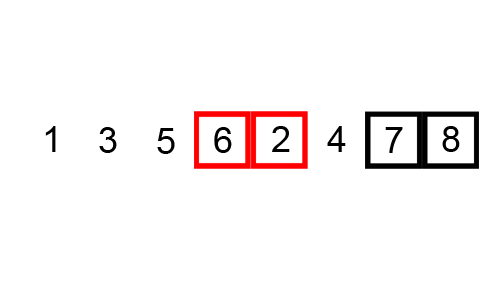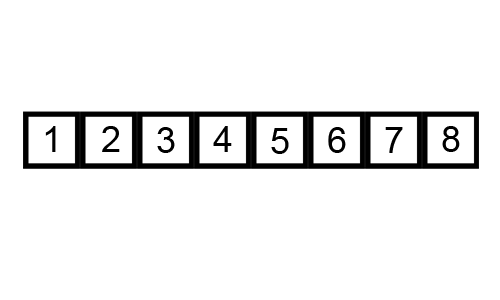
예제 코드
def bubble_sort(arr):
n = len(arr)
for i in range(n):
done_sort = True
for j in range(n -i -1):
if arr[j] > arr[j+1]: #버블 정렬
arr[j], arr[j+1] = arr[j+1], arr[j] #스왑
print(input_arr)
done_sort = False # 스왑될 때마다 False 를 반환
if done_sort: #스왑되지 않으면 for문을 나오게 되어 True로 바뀜
break # done_sort가 True 일 때 순회 종료
return arr
input_arr = [8,2,6,4,5]
print("before: ",input_arr)
bubble_sort(input_arr)
print("after:", input_arr)정렬이 되었는지 판단하는 기준은 done_sort(변수)로 두었다.
교환이 일어났을 때 False로 변경하고 그렇지 않은 경우는 for문을 나와 True로 값이 변경되어 break를 통해 전체 순회를 종료하게 하였다.
기본적으로 0~n-1 까지 순회하고, 각 순회에서 1회씩 증가할 때 마다
0~n-1-1, 0~n-2-1 ... 0~n-i-1 만큼 이동하면서 앞뒤 요소를 비교하여 큰 값을 교환해주는 방식이다.
출력 결과
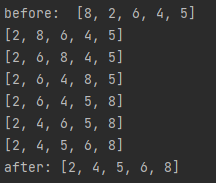
시간복잡도
1회 순회에서 (n-1)번의 비교가 일어난다. 그리고 다음번은 n-2번... 그 다음은 n-3 ...n-4...2...1... 순회가 종료된다.
따라서 이 순회를 모두 더하면 (n-1) + (n-2) + (n-3) + ... + 3 + 2 + 1 = n(n-1)/2 가 되고 이를 간단하게 n의 제곱이라고 표현한다. 따라서 시간복잡도는 O(n²)이며, 느린 성능을 가진다는 것을 알 수 있다.
2. 삽입 정렬 (Insertion Sort)
거품 정렬과 비슷하게 삽입 정렬도 직관적으로 구현하기 쉽다. 하지만 거품 정렬과는 다르게 리스트 내 하나의 요소를 선택해 다른 요소와 비교하여 알맞은 위치에 '삽입'하는 정렬이다.
따라서, 삽입 정렬은 하나의 요소를 알맞은 위치에 삽입하기 위해 순회한다.
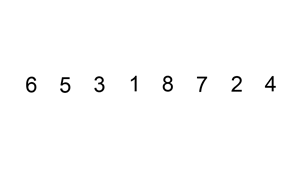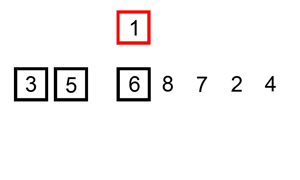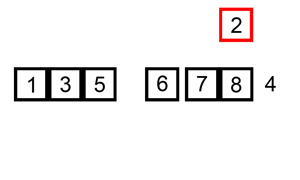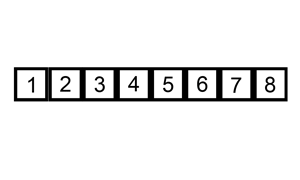
예제 코드
def insert_sort(arr):
n = len(arr)
for i in range(1,n): # 1 ~ n-1 번째 까지 돈다.
key_item = arr[i] #키값은 i번째에 있는 것으로 설정
j = i - 1 # J는 i 바로 앞 번째
while j >= 0 and arr[j] > key_item: #j가 0보다 크고 arr[j] (i 앞 번째인 J번째가 key_item (arr[i] 앞번째)보다 클 경우)
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key_item # while문을 통과하면 다음 값을 key로 설정
print("key", key_item,"sorted arr",arr[:i+1])
return arr
input_arr = [8, 2, 6, 4, 5]
print("before:", input_arr)
insert_sort(input_arr)
print("after:", input_arr)
처음 순회는 1부터 n-1까지 진행한다. 요소가 하나만 있는 경우 이미 정렬된 상태로 보기 때문이다.
다음 내부 while문을 통해 순회하는데, 현재 위치의 선택된 값(i 인덱스)을 이전 요소부터 맨 앞 요소 (0 인덱스) 까지 비교하여 0의 인덱스에 도달하거나 key_item의 값이 비교되는 j 인덱스 값보다 작다면 순회를 중단한다.
그렇게 되면 앞 요소가 다음 인덱스로 이동했거나 key_item이 현재 가장 크므로 j 값이 그래도라 해당 위치로 삽입된다.
출력 결과
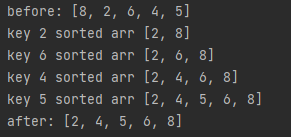
이렇게만 설명하면 이해하기 조금 어려우므로 덧붙여 설명하겠다.
코드를 기준으로 살펴보면,
1) i = 1, key_item = 2, j = 0
arr[0] > key_item 이기 때문에 a[1] = a[0] => [8,8,6,4,5]
j = -1 이 되므로 순회 종료
arr[1] = key_item => [2,6,8,4,5]
2) i = 2, key_item = 6, j = 1
arr[1] > key_item 이기 때문에 a[2] = a[1] => [2,8,8,4,5]
j = 0 이 되고 (while문), arr[0] 보다 key_item 이 크므로 순회 종료
arr[2] = key_item => [2,6,8,4,5]
3) i = 3, key_item = 4, j = 2
arr[2] > key_item이기 때문에, a[3] = a[2] => [2,6,8,8,5]
j = 1 이 되고 (while문), arr[1] > key_item 이기 때문에, a[2] = a[1] => [2,6,6,8,5]
j = 0 이 되고 (while문), arr[0] 보다 key_item이 크기 때문에 순회 종료
arr[1] = key_item => [2,4,6,8,5]
4) i = 4, key_item = 5, j = 3
arr[3] > key_item이기 때문에, a[4] = a[3] => [2,4,6,8,8]
j = 2 가 되고 (while문), arr[2] > key_item 이기 때문에, a[3] = a[2] = > [2,4,6,6,8]
j = 1 이 되고 (while문), arr[1] 보다 key_item이 크기 때문에 순회 종료
arr[2] = key_item => [2,4,5,6,8]
2750번: 수 정렬하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
문제
N개의 수가 주어졌을 때, 이를 오름차순으로 정렬하는 프로그램을 작성하시오.
입력
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
출력
첫째 줄부터 N개의 줄에 오름차순으로 정렬한 결과를 한 줄에 하나씩 출력한다.
버블 정렬
def bubble_sort(arr):
n = len(arr)
for i in range(n): # 0, 1, 2, 3 ... n-1까지의 수
done_sort = True
for j in range(n -i -1):
if arr[j] > arr[j+1]: # 두 수 중 왼쪽에 있는 수가 더 크면
arr[j], arr[j+1] = arr[j+1], arr[j] # 큰 수를 오른쪽으로 자리를 바꿔줌
done_sort = False
if done_sort:
break
return arr
n = int(input())
arr_list = [0] * n
for i in range(n):
tmp = int(input())
arr_list[i] = tmp
arr_list = bubble_sort(arr_list)
for i in arr_list:
print(i)
삽입 정렬
def insert_sort(arr):
n = len(arr)
for i in range(1,n): # 1 ~ n-1 번째 까지 돈다.
key_item = arr[i] #키값은 i번째에 있는 것으로 설정
j = i - 1 # J는 i 바로 앞 번째
while j >= 0 and arr[j] > key_item: #j가 0보다 크고 arr[j] (i 앞 번째인 J번째가 key_item (arr[i] 앞번째)보다 클 경우)
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key_item # while문을 통과하면 다음 값을 key로 설정
return arr
n = int(input())
arr_list = [0] * n
for i in range(n):
tmp = int(input())
arr_list[i] = tmp
arr_list = insert_sort(arr_list)
for i in arr_list:
print(i)
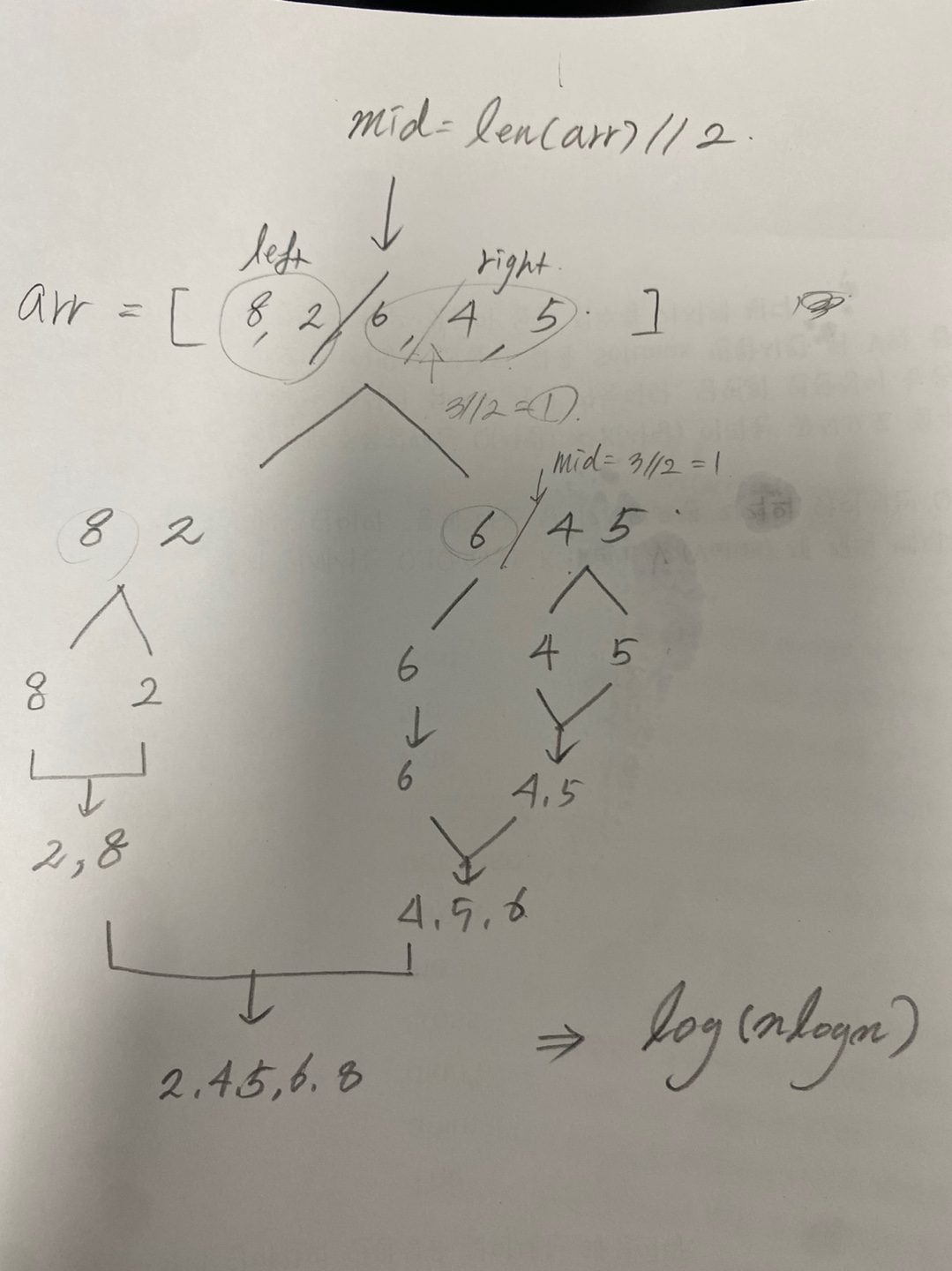
3. 병합 정렬 (Merge Sort)
거품 정렬과 삽입 정렬보다 높은 효율을 보이는 정렬 알고리즘이다.
병합 정렬은 분할 정복(Divide and Conquer) 접근을 기반으로 복잡한 문제를 해결할 때 사용하는 강력한 알고리즘 기술이다. 분할 정복을 이해하기 위해서는 재귀를 이해하는 것이 필요하다.
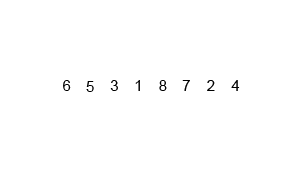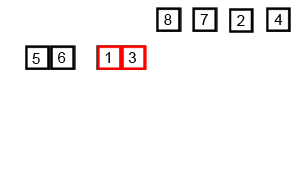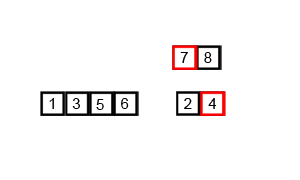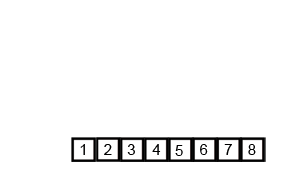
- 분할 정복과 재귀를 이용한 알고리즘으로 O(n log n)의 시간 복잡도를 가지고 있어 괜찮은 성능을 보여 준다.
- 반으로 쪼개고 다시 합치는 과정에서 그룹을 만들어 정렬하게 되며 이 과정에서 2n 개의 공간이 필하다.
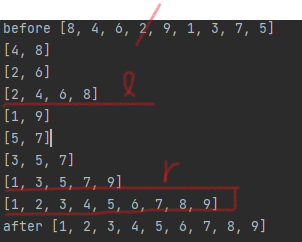
- 합쳐지는 과정은 다음같다.
[1,4][2,3] (1과 2 비교) -> 1 선택, 완성된 배열은 [1]
[4][2,3] (4와 2 비교) -> 2 선택, 완성된 배열은 [1,2]
[4][3] (4와 3 비교) -> 3 선택, 완성된 배열은 [1,2,3]
[4][] -> 남는 4 선택, 완성된 배열은 [1,2,3,4]
예제 코드
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
left_arr = merge_sort(arr[:mid]) # 재귀
right_arr = merge_sort(arr[mid:]) # 재귀
merged_arr = []
l = r = 0
while l < len(left_arr) and r < len(right_arr):
if left_arr[l] < right_arr[r]:
merged_arr.append(left_arr[l])
l += 1
else:
merged_arr.append(right_arr[r])
r += 1
#비교가 끝나고 마지막에 남은 부분을 붙여줌
merged_arr += left_arr[l:]
merged_arr += right_arr[r:]
return merged_arr
input = [8,2,6,4,5]
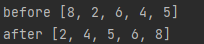
print("before",input)
print("after",merge_sort(input))출력 결과
4. 퀵 정렬 (Quick Sort)
병합 정렬과 비슷하게 분할 정복 방법을 이용한 방식이다. 다른 점은 입력 리스트를 두 리스트로 나눌 때, 한 쪽은 특정 값보다 작은 값만 모으고 다른 하나는 특정 값보다 큰 값만 모은다. 이를 재귀적으로 완전히 정렬될 때 까지 진행한다.
특정 값을 퀵 정렬에서 피벗(Pivot)이라고 부르는데 피벗을 결정하는 방식에 따라 성능 차이가 발생하기도 한다.
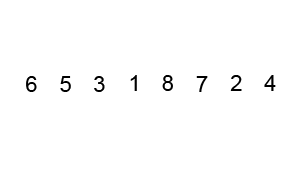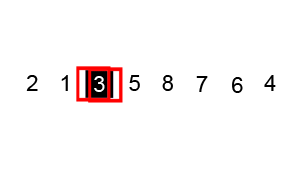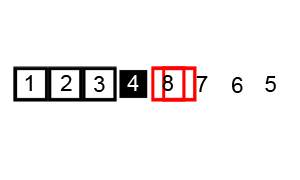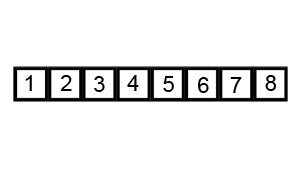
- 병합 정렬과 마찬가지로 분할 정복 알고리즘으로 평균적으로 빠른 속도를 수행한다.
- 추가적인 메모리가 공간이 필요 없다는 장점을 가졌다.
- 병합 정렬은 균등하게 분할하였다면 퀵 정렬은 Pivot을 설정하고 그 기준으로 정렬한다.
- 다른 정렬 알고리즘보다 빠르며 많은 언어의 정렬 내장 함수로 퀵 정렬을 수행한다.
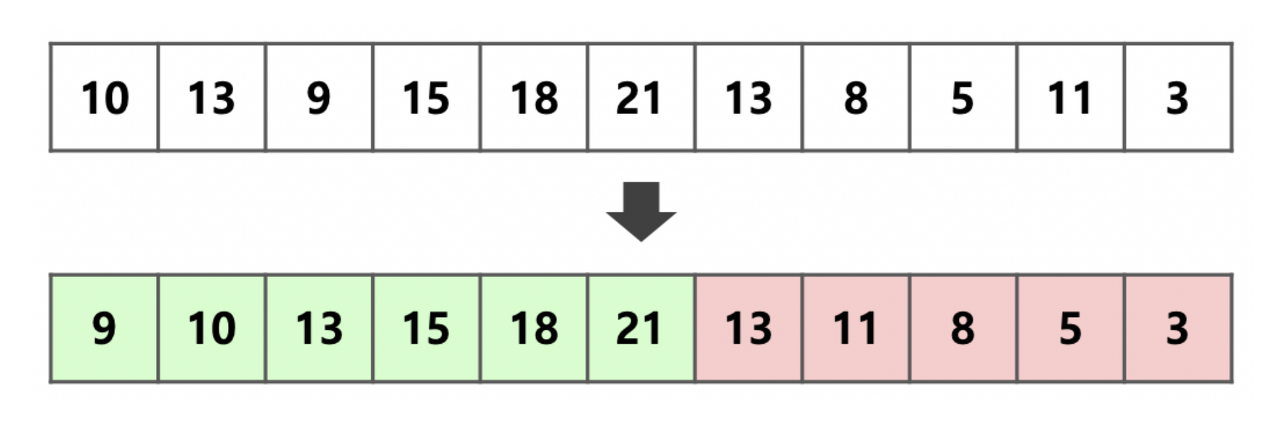
입력 리스트를 나누는 것을 파티셔닝(Partitioning, 분할) 이라고 부른다. 분할할 때마다 피벗을 선택하여 두 부류 (작은 값 - low, 큰 값 high) 로 나누는 작업을 한다.
각 파티셔닝마다 피벗 값을 결정해야하는데 많은 고민이 필요하다. 만약 피벗 값이 리스트 마지막 요소로 선택되어 있는 경우, 이미 정렬된 리스트라면 계속 작은 값에 남은 요소가 다 들어가게 되므로 시간복잡도가 O(n²)이 된다.
이것을 방지하기 위해 무작위로 피벗을 결정하여 최악의 경우를 최소화하는 방향이나 중간 값을 찾아 low/ high 분배를 하면 안정적으로 O(nlogn)의 시간 복잡도를 가질 수 있다.
퀵 정렬 피벗은 선택에 따라 성능이 크게 달라진다.
from random import randint
def quicksort(arr):
arr_len = len(arr)
if arr_len <2:
return arr
low, same, high = [], [], []
pivot = arr[randint(0,arr_len-1)] # 피벗 값은 맨앞이나 맨 뒤 중 랜덤으로
for item in arr:
if item < pivot:
low.append(item)
elif item == pivot:
same.append(item)
elif item > pivot:
high.append(item)
print("sort", quicksort(low) + same + quicksort(high))
return quicksort(low) + same + quicksort(high)
input_array = [8,2,6,4,5]
print("before:",input_array)
print("after:",quicksort(input_array))
위의 코드는 최악의 경우 (시간복잡도가 O(n²))가 되는 경우가 발생하지 않게 하는 방법 중 하나로 배열 내 무작위 값을 선택해 피벗으로 이용하는 방법을 구현하였다.
퀵 정렬은 피벗 값을 무조건 중앙 값으로 선택할 수 있다면 low, high가 정확히 반으로 나누어지기 때문에 안정적으로 O(nlogn)의 성능을 유지할 수 있다.
피벗 잡는 방법
- 난수(Random Quick Sort), 중위법
- 가장 쉽고 비효율적인 방법.
- 배열 중에 3개나 9개의 원소를 골라서 이들의 중앙값을 피벗으로 고르는 것
- Visual c++과 gcc에서 구현하고 있는 방법이라고 한다.
- 이 방법을 사용하더라도 최악의 경우가 나올 수 있지만 그 경우가 극히 드물게 된다.
- 인트로 정렬
- 재귀 깊이가 어느 제한 이상으로 깊어질 경우 힙 정렬 알고리즘을 사용하여 항상 O(n log n)을 보장해주는 방법
5. 팀 정렬(Tim Sort)
python에서의 정렬 함수 sorted()와 list.sort()에 사용된 정렬 알고리즘은 Timsort, 팀정렬이다.
팀 정렬은 삽입정렬 + 병합정렬을 섞어 사용한다. 다만, 삽입 정렬의 비교 연산을 줄이기 위해 선택된 요소의 알맞은 위치 탐색을 선형 탐색(Linear Search)이 아닌 이진탐색(Binary Search)으로 하고 이 위치에 요소 삽입을 진행한다.
* 선형 탐색(Linear Search) 시간 복잡도: O(n)
* 이진탐색(Binary Search) 시간 복잡도: O(logn)
성능은 당연히 이진탐색이 더 좋다.
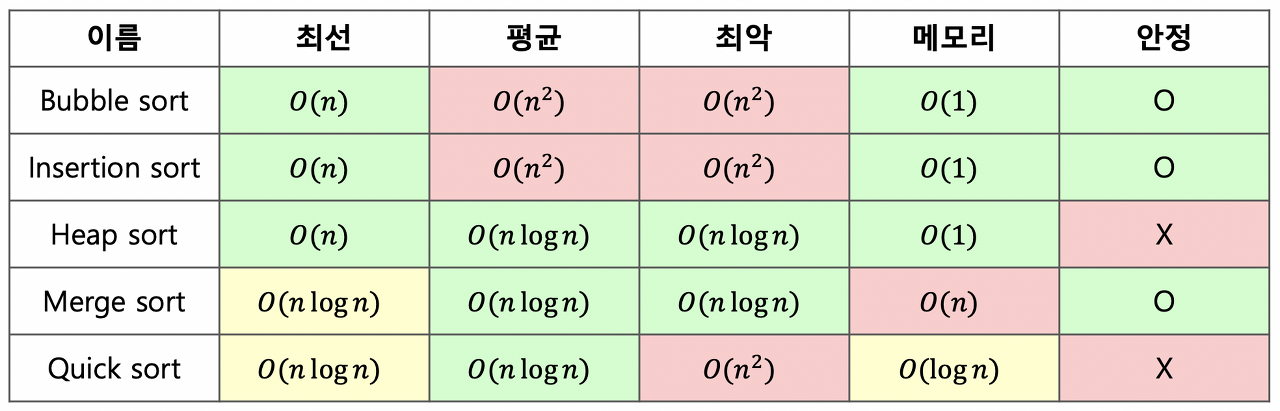
정렬 알고리즘 종류와 설명(파이썬 예제)
정렬은 데이터를 순차적으로 나열하는 방법으로 정렬 알고리즘 별로 수행 성능이 크게 차이납니다. 버블 정렬, 삽입 정렬, 선택 정렬, 병합 정렬, 퀵 정렬을 설명드립니다.
velog.io
[python] 파이썬의 정렬, Tim Sort
Tim Sort python에서의 정렬 함수 sorted() 와 list.sort() 에 사용된 정렬 알고리즘은 Timsort, 팀정렬입니다. 팀정렬은 파이썬 핵심 개발자인 팀 피터스에 의해서 Cpython에서 처음으로 구현되었으며 2009년
ssungkang.tistory.com
참고 서적
 |
쓰면서 익히는 알고리즘과 자료구조 |
'python > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 연결 리스트 Linked-List / Python 파이썬 (0) | 2022.05.12 |
|---|---|
| [자료구조] 스택, 큐, 재귀함수 / Python 파이썬 (0) | 2022.05.06 |
| [알고리즘] 8-Puzzle (8 퍼즐) BFS, DFS 구현 / Python 파이썬 (0) | 2022.04.28 |
| [자료구조] 해시, 해시법(hashing) / Python 파이썬 (0) | 2022.04.12 |
| [자료구조] 검색 알고리즘 (선형 검색/ 이진 검색) / Python 파이썬 (0) | 2022.04.12 |