트리 (Tree)

트리(Tree)는 계층적 데이터를 저장하고 활용하기 위한 자료구조이다.
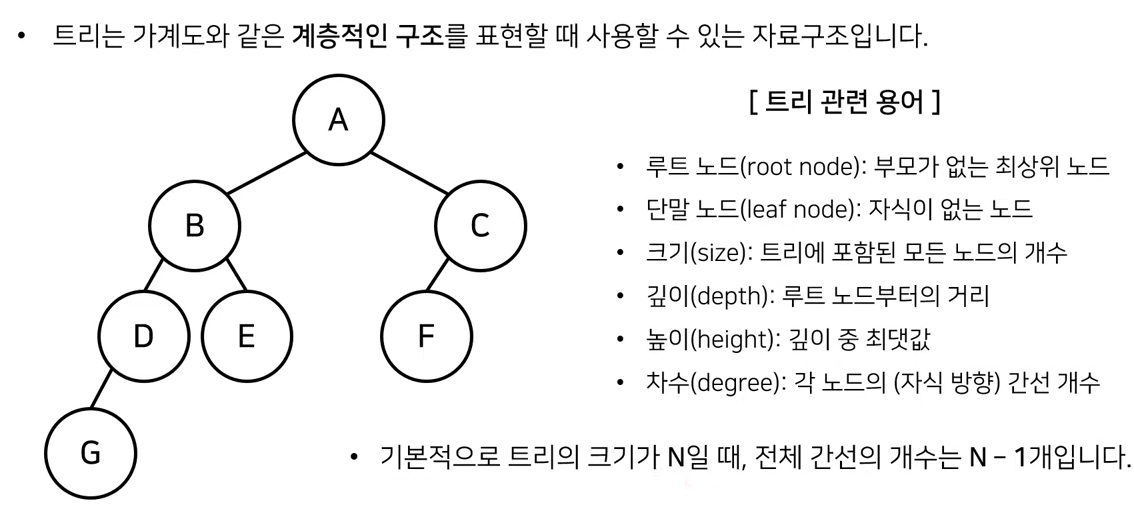
트리의 특징
- 트리는 비선형적(none-linear) 구조의 자료구조다.
- 트리는 연결리스트와 동일하게 노드(Node)를 가지고있다. 각 노드는 엣지(Edge)로 연결되어있다.
- 각 노드는 부모(Parent) / 자식(Child) 관계를 가진다.
- 트리 자료구조의 구성 요소:
- 루트(root)노드: 가장 꼭대기에 있는 도드
- 잎새(leaf)노드: 트리의 마지막 노드, 즉 자식이 없는 노드
- 높이(height = Level): 높이는 잎새(leaf) 노트부터의 경로 길이
- 깊이(depth): 깊이는 루트에서 노드로의 경로 길이
이진 트리(Binary Tree)
그 중, 자식 노드가 최대 2개까지만 붙는 트리를 이진트리(Binary tree)라고 한다.
이 두 개의 노드는 왼쪽 자식과 오른쪽 자식으로 분류한다.
*모든 트리가 이진 트리는 아니다. 자식이 3개붙은 트리는 Ternary tree가 되며, 4개씩 붙는 경우도 있다.
이진 트리는 자료의 삽입, 삭제 방법에 따라 세가지가 있다.
- 정 이진 트리(Full binary tree)
- 완전 이진 트리(Complete binary tree)
- 포화 이진 트리(Perfect binary tree)

이진 트리 표현
class Node:
def __init__(self,data):
self.left = None
self.right = None
self.data = data
# repr 함수는 어떤 객체의 ‘출력될 수 있는 표현’
# (printable representation)을 문자열의 형태로 반환한다.
def __repr__(self):
return str(self.data)
root = Node(11)
print(root)
'''실행결과: 1'''
이진 트리는 다음(next) 노드가 아닌 왼쪽과 오른쪽 2개의 자식(child) 노드를 가리킨다는 점만 빼고 연결리스트의 구성과 비슷하다.
* __repr__ :
- repr은 ‘Representation’의 약자로 이 단어는 ‘표현하다’라는 뜻을 가지고 있다.
- repr 함수는 어떤 객체의 ‘출력될 수 있는 표현’(printable representation)을 문자열의 형태로 반환한다.
* __str__:
- str은 입력 받은 객체의 문자열 버전을 반환하는 함수다.
이진 탐색 트리(Binary Search Tree)

기본 연산은 추가(insert), 탐색(find), 삭제(de-lete)이다.
추가(insert)
탐색(find)
삭제(de-lete)
트리의 순회 (Tree Traversal)
- 트리 자료구조에 포함된 노드를 특정한 방법으로 한 번식 방문하는 방법
- 트리의 정보를 시각적으로 확인할 수 있다.
트리 순회 방법은 세가지가 있다.
- 전위 순회(pre-order traverse): 루트를 먼저 방문
- 중위 순회(in-order traverse): 왼쪽 자식을 방문한 뒤에 루트를 방문
- 후위 순회(post- order traverse): 오른쪽 자식을 방문한 뒤에 루트를 방문

class Node:
def __init__(self,data,left_node,right_node):
self.left_node = left_node
self.right_node = right_node
self.data = data
# 전위 순회(Preorder Traversal)
def pre_order(node): # 부모 노드부터 순회한다.
print(node.data, end = '')
if node.left_node != None:
pre_order(tree[node.left_node])
if node.right_node != None:
pre_order(tree[node.right_node])
# 중위 순회(Inorder Traversal)
def in_order(node): # 왼쪽 자식 노드부터 순회한다.
if node.left_node != None:
in_order(tree[node.left_node])
# 왼쪽 자식 노드 탐색 후 출력
print(node.data, end = '')
if node.right_node != None:
in_order(tree[node.right_node])
# 후위 순회(postorder Traversal)
def post_order(node):
if node.left_node != None:
post_order(tree[node.left_node])
if node.right_node != None:
post_order(tree[node.right_node])
# 오른쪽 자식노드 탐색 후 출력
print(node.data, end='')
n = int(input())
tree = {}
for i in range(n):
data, left_node, right_node = input().split()
# data의 left와 right 노드에 None 이면 해당 데이터가 자식 노드임
if left_node == "None":
left_node = None
if right_node == "None":
right_node = None
# 딕셔너리에 저장
tree[data] = Node(data,left_node,right_node)
pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])입출력 결과
'''
입력 예시
7
A B C
B D F
C F G
D None None
E None None
F None None
G None None'''
Reference
- 이미지[1] https://spaghetti-code.tistory.com/23
- 이미지[3] https://towardsdatascience.com/5-types-of-binary-tree-with-cool-illustrations-9b335c430254
- 이미지[2],[4],[5] https://www.youtube.com/watch?v=i5yHkP1jQmo
'python > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 동적계획법 Dynamic Programming / 파이썬 Python (0) | 2022.08.03 |
|---|---|
| [자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) / Python 파이썬 (0) | 2022.07.29 |
| [자료구조] 연결 리스트 Linked-List / Python 파이썬 (0) | 2022.05.12 |
| [자료구조] 스택, 큐, 재귀함수 / Python 파이썬 (0) | 2022.05.06 |
| [알고리즘] 정렬 알고리즘 / Python 파이썬 (0) | 2022.05.03 |