이 게시글은 김성범 교수님의 유튜브 강의를 정리한 내용입니다.
내용과 사진의 각 출처는 김성범 교수님께 있음을 미리 알립니다.
해당 게시글 강의 영상 : https://www.youtube.com/watch?v=W-DNu8nardo
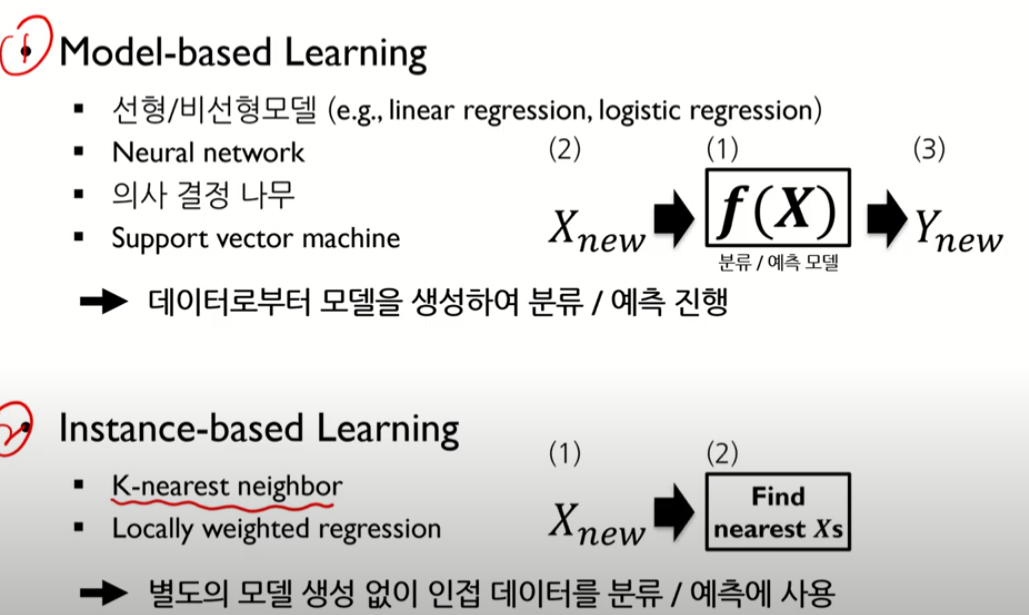
KNN은 모델이 없는 것
데이터가 어떤 것에 가까운지 분류하고 예측하는 것
1-nearest neighbor: 가장 가까운 데이터 1개의 이웃을 정의
3-nearest neighbor: 가장 가까운 데이터 3개의 이웃을 정의

새로운 데이터의 Y값을 알아내는 것이 문제임

가까운 순서대로 거리를 구하고,
새로운 예측 데이터에대해 수행한다.
KNN 알고리즘의 구분 및 특징

Instance-based Learning
각각의 관측치만을 이용하여 새로운 데이터에 대한 예측 진행
Memory-based Learning
모든 학습 데이터를 메모리에 저장한 후, 이를 바탕으로 예측 시도
Lazy Learning
모델을 별도로 학습하지 않고, 테스팅 데이터가 들어와야 비로소 작등하는 게으른 알고리즘
Linear Model (Classification) VS KNN
Linear Model (Classification): 말 그대로 선형이다.
KNN: 비선형임
KNN은 모델을 만드는 것이 아님. 모델의 형태는 정해져있지 않고, 방법론 및 알고리즘이라고 일컫는다.
KNN 분류
"내 이웃의 다수의 패턴으로 따라간다."
관측치를 정하고, 그 관측치에서 가까운 거리에 있는 이웃데이터를 탐색한다.


KNN 분류 알고리즘 순서

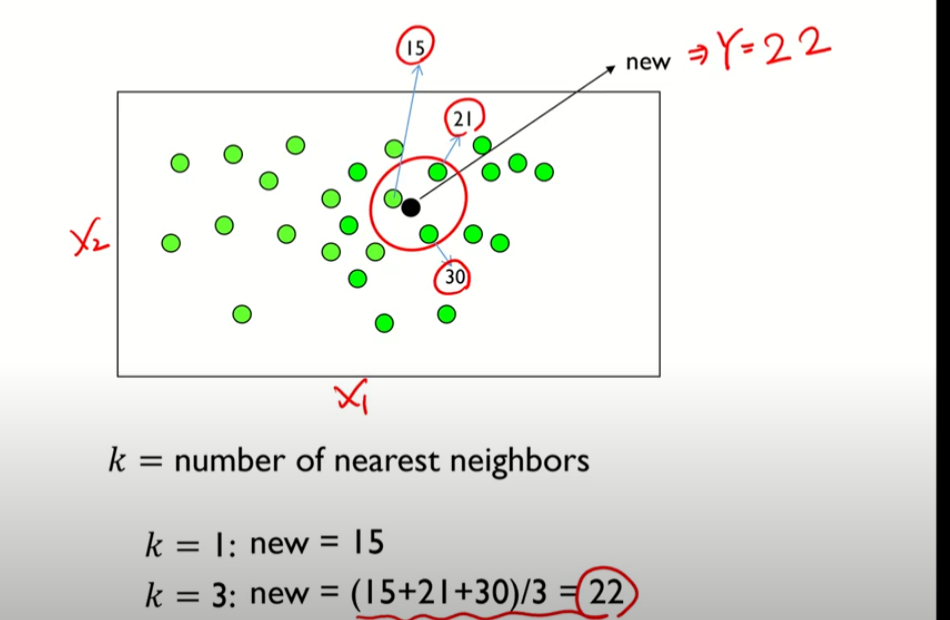
근접한 이웃이 2개이상일 때, 해당 값은 평균으로 예측한다.
평균으로 예측하는 것이 가장 정확하다는 학자들의 의견이 분분해서
평균으로 주로 한다고한다.
예제
평점을 예측하는 문제
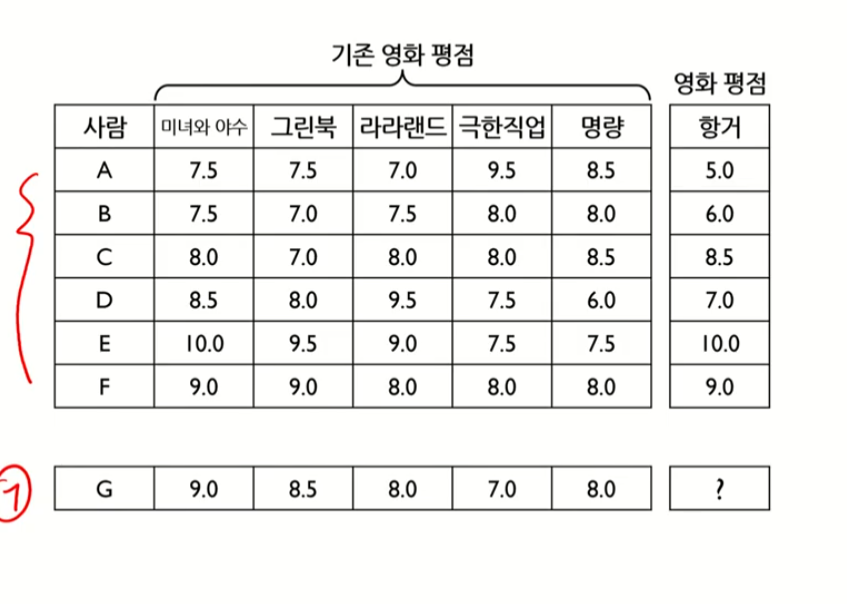
G고객과 가장 영화 패턴이 비슷한 사람은 F (거리가 비교적 짧음)
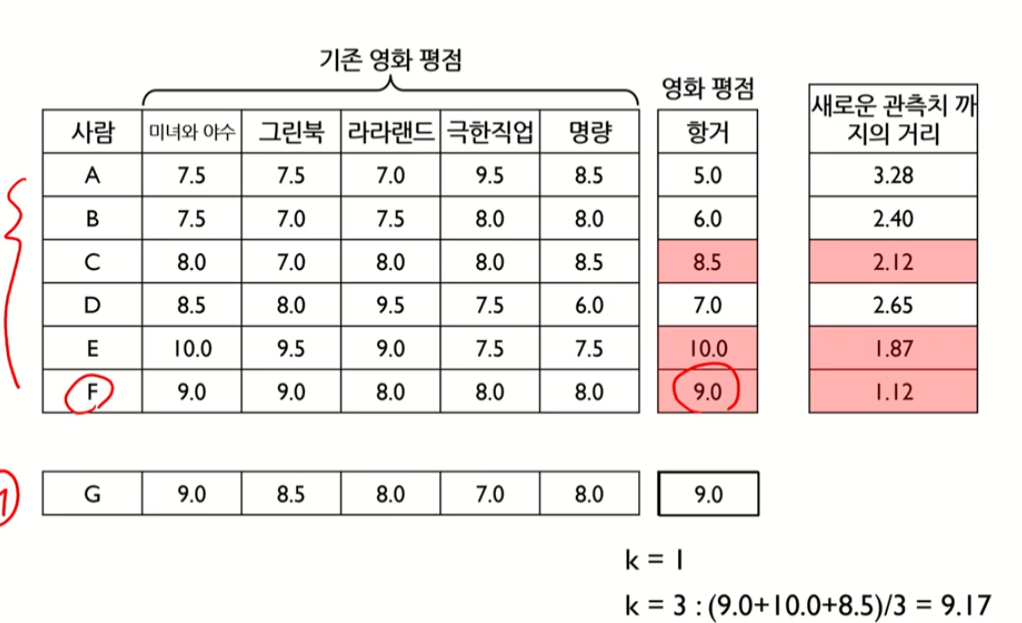
KNN 예측 알고리즘

KNN 하이퍼파라미터

KNN에서는 하이퍼파라미터로 k, Distance Mearsures 두가지가 있다.
K = 인접한 데이터의 개수
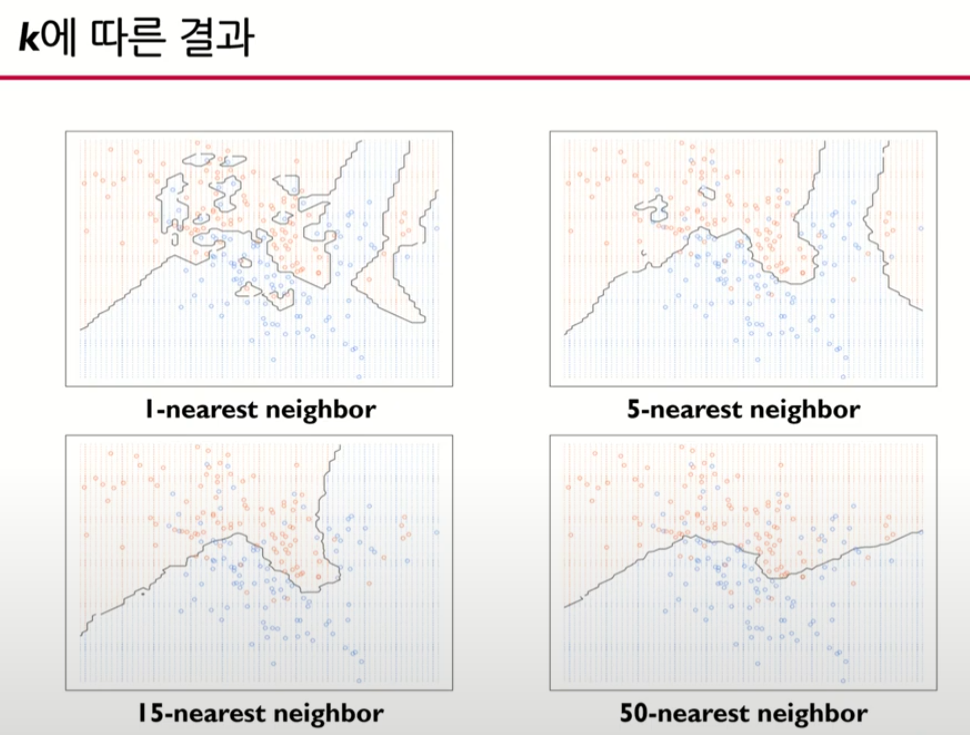
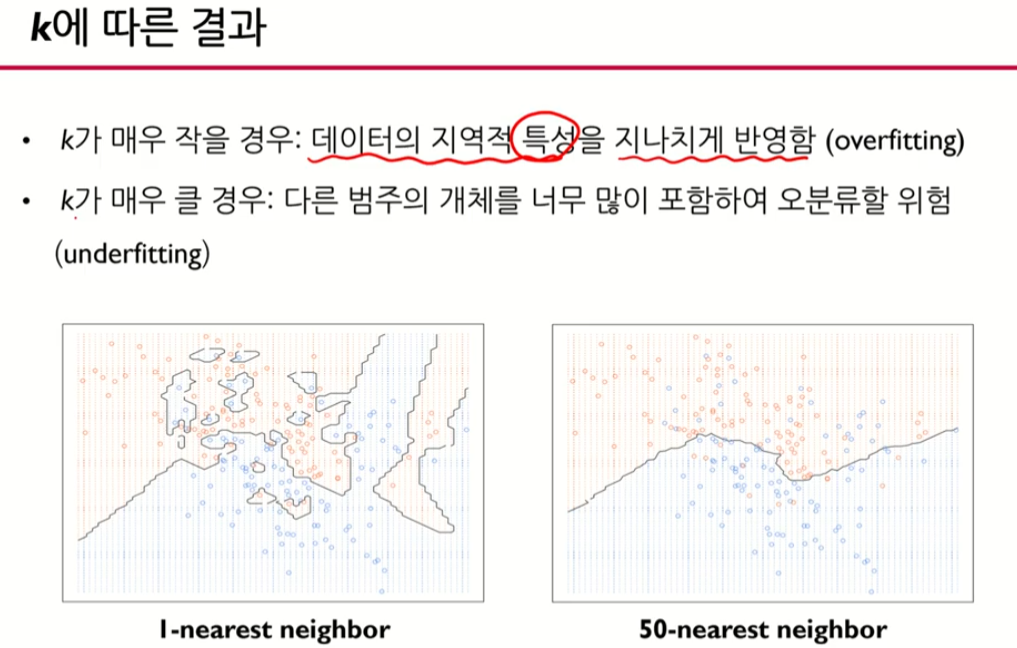
K가 적으면 Local 패턴으로 가장 정교하게 나옴
K 의수를 늘려나갔을 때 Global 하게 나옴
따라서 K의 지정가능 범위는
1<= K <= 전체 데이터 갯수
K 선택 방법

Ci 값과 ^ci 값은 같을 수록 좋음
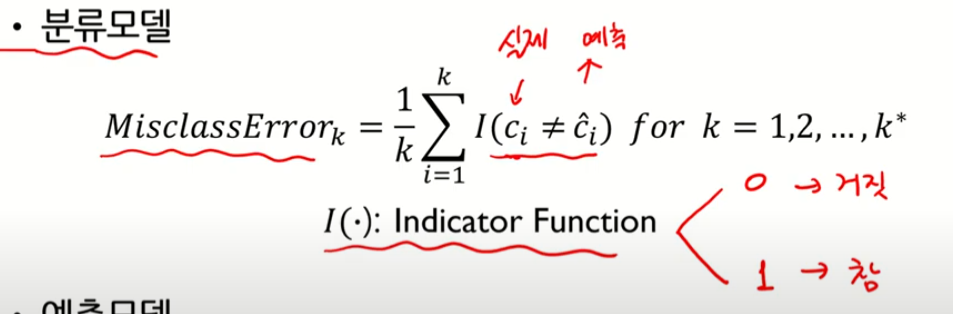
참이면 다른 것
거짓이면 비슷한 것
K 선택 방법
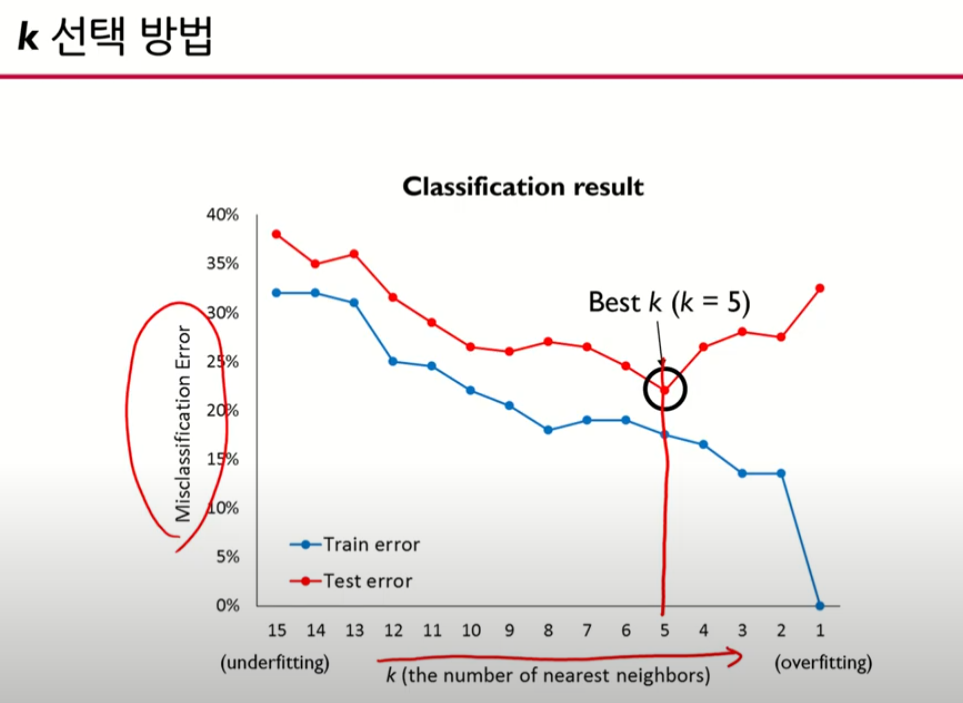
error가 동시에 작아지는 지점에서 해당 K값을 사용
거리측도
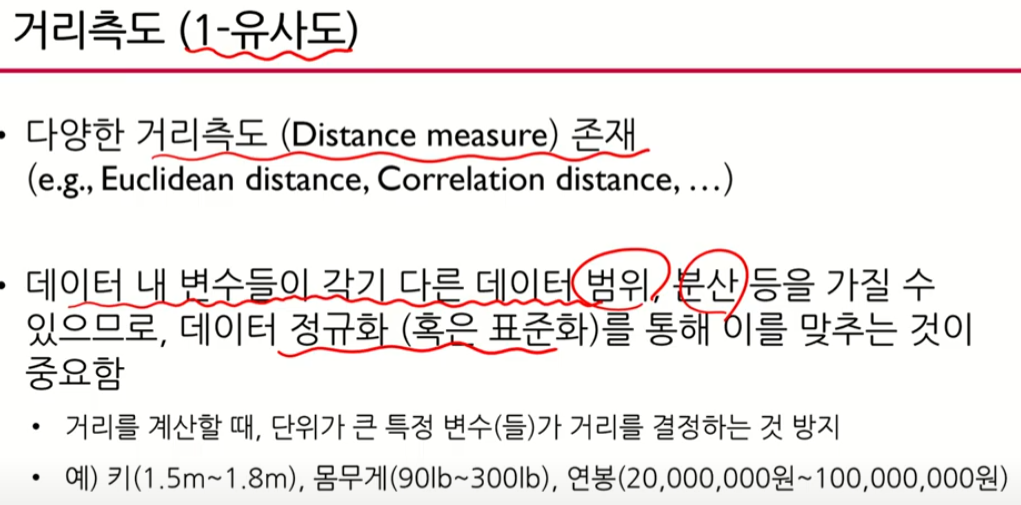
1. Euclidean Distance
2. Manhattan Distance
3. Mahalnobis Distance
4. Correlation Distance
- Pearson Correlation
- Spearman Rank Correlation
자세한 거리 측도는 해당 게시글 참조
https://sillon-coding.tistory.com/172
[Data Science from Scratch] Ch 4, 5, 6 additional note
참고 서적 도서명: Data Science from Scratch (밑바닥부터 시작하는 데이터 과학) 저자 : Joel Grus 출판 : 프로그래밍 인사이트 Ch 4. 선형대수 4.1 거리 유사도 측정방법 Euclidean Distance 두 점 p, q사..
sillon-coding.tistory.com
1. Euclidean Distance

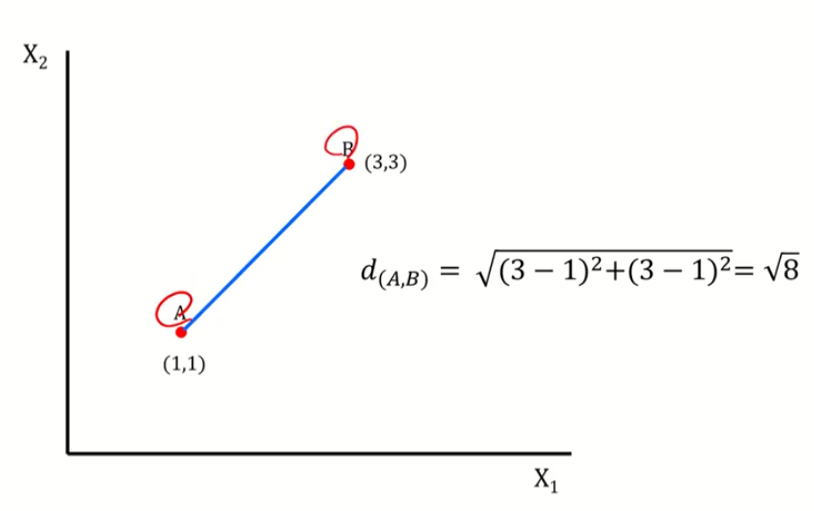
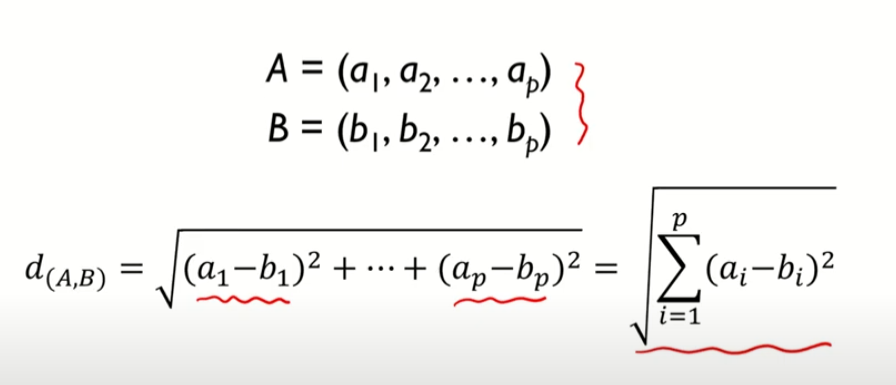
다차원데이터여도 유클리드 거리를 이용하면 결국 값은 1X1로 나옴
2. Manhattan Distance
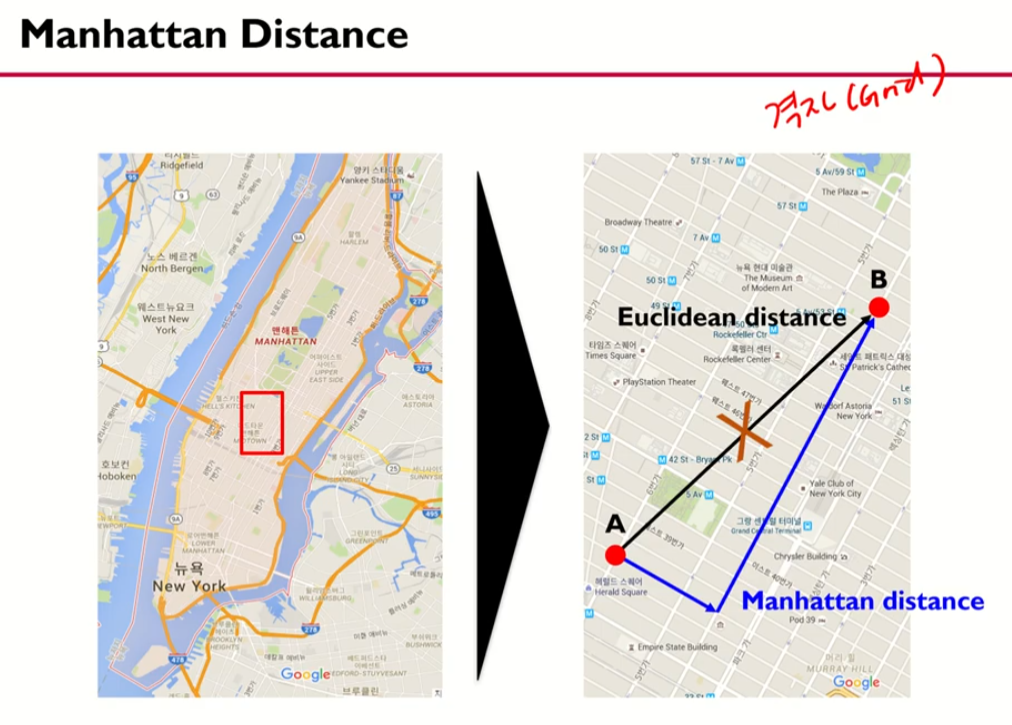
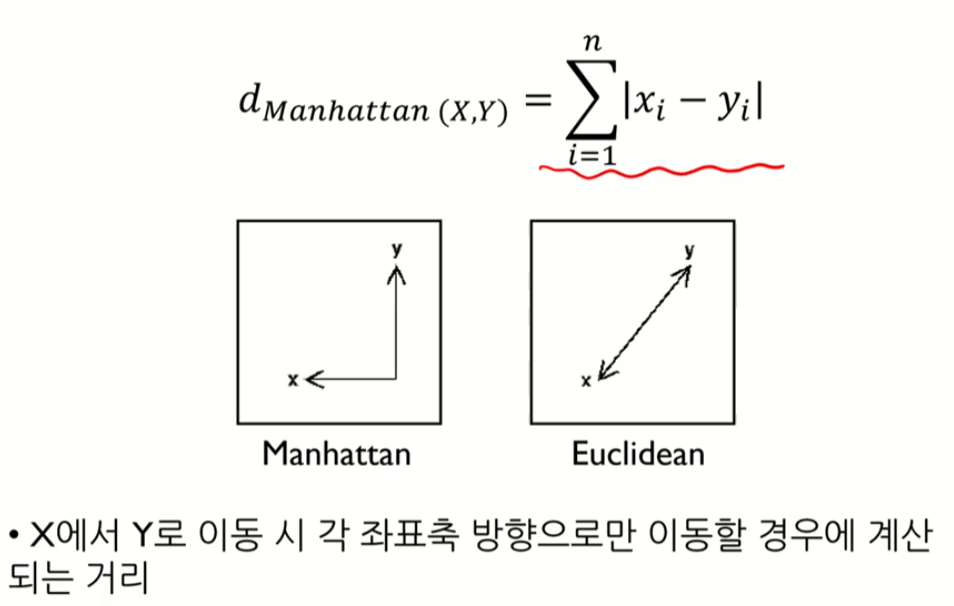
3. Mahalnobis Distance (마할라노비스 거리)

identity matrix 는 단위행렬
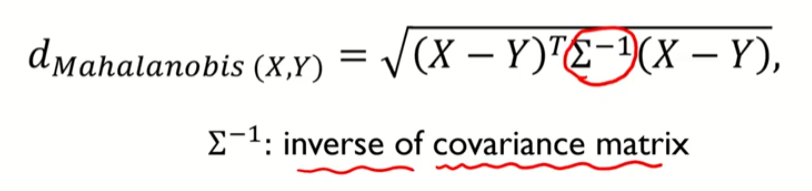
공분산 행렬의 역행렬
분산이 커지면 작은 값을 곱해주고, 분산이 작아지면 큰 값을 곱해준다.

마할라노비스의 제곱은 타원이 된다.
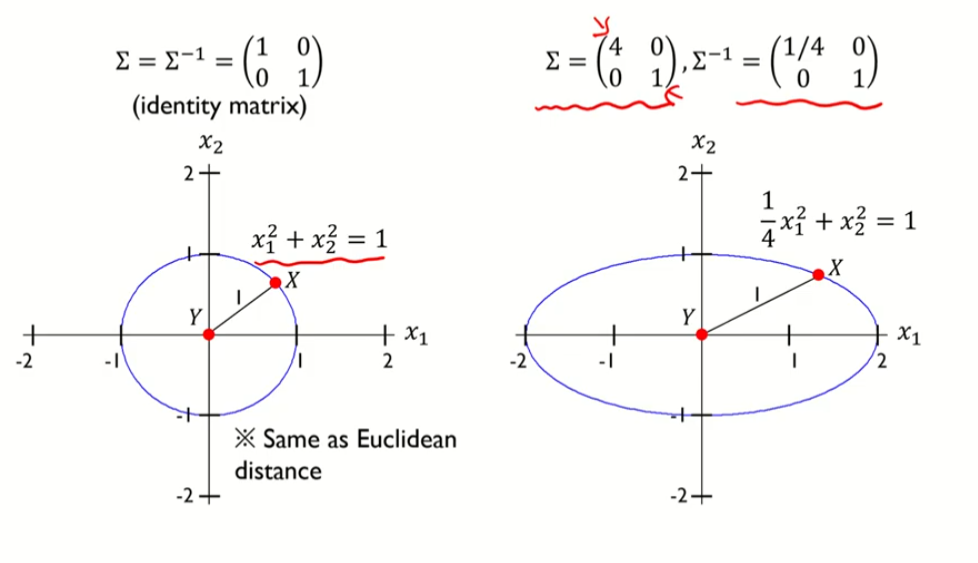

공분산을 고려한 자취의 방정식은 휘어진 타원의 방정식이 된다.
C값을 변동하면 타원이 어떻게 변하는지 살펴보자.

유클리디안 관점과 마할라노비스 관점의 비교
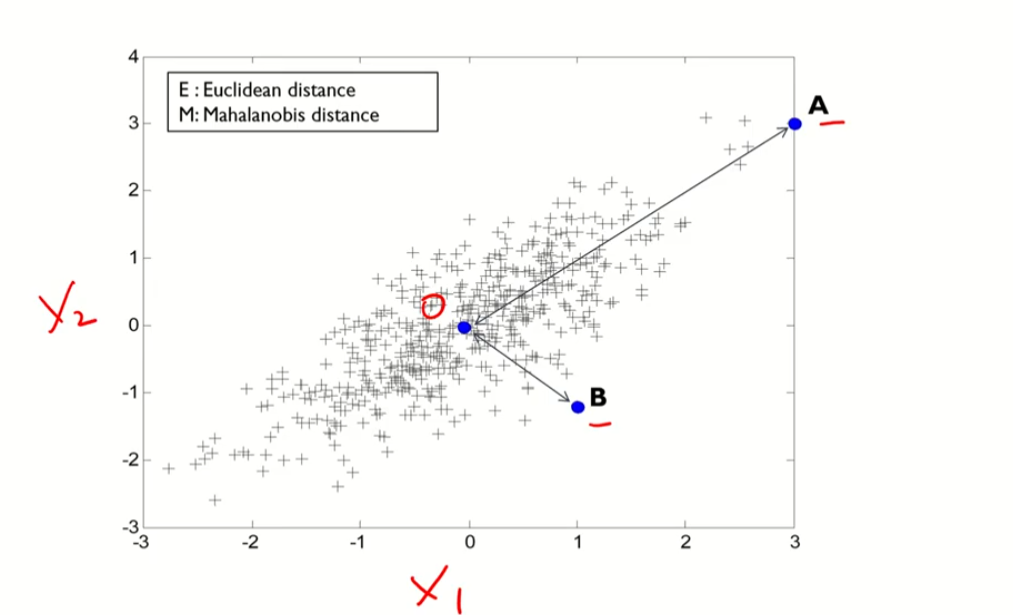
유클리디안 관점
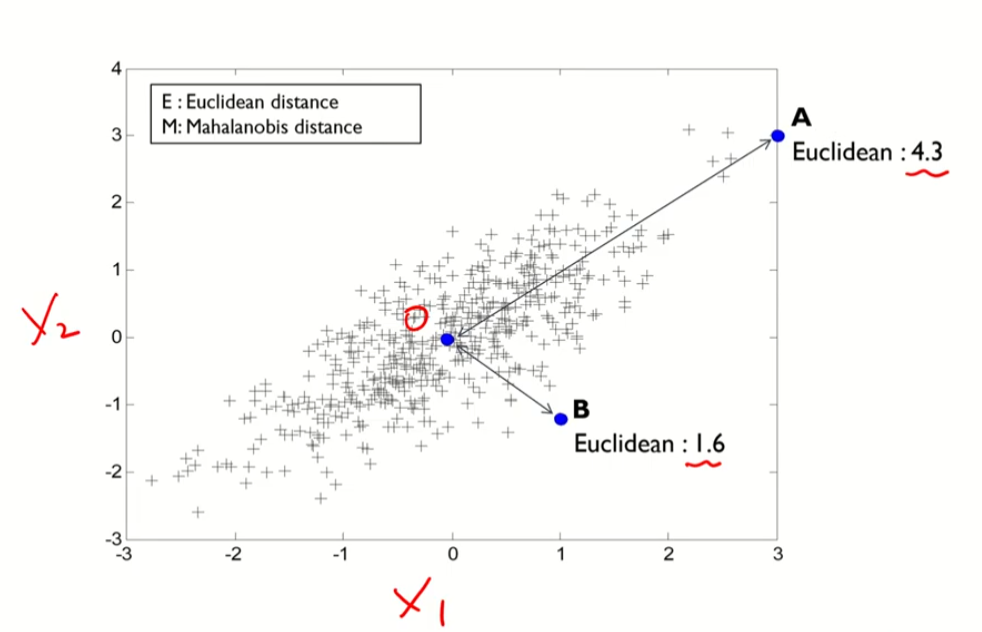
MAX(A,B) = A,즉 A가 더 멀다.
마할라노비스 관점
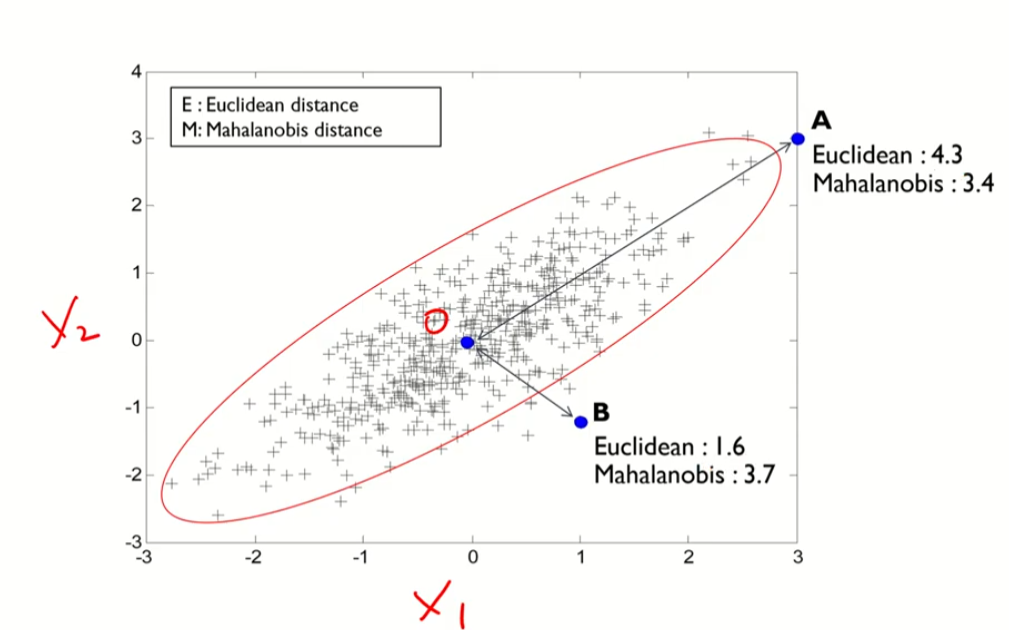
마할라노비스틑 공분산이 큰 경우임(상관관계)
A는 상관관계를 고려한다면 오른쪽 위 방향으로 감

B는 상관관계에서 다른 방향임. 따라서 B가 더 멀다.
4. Correlation Distance
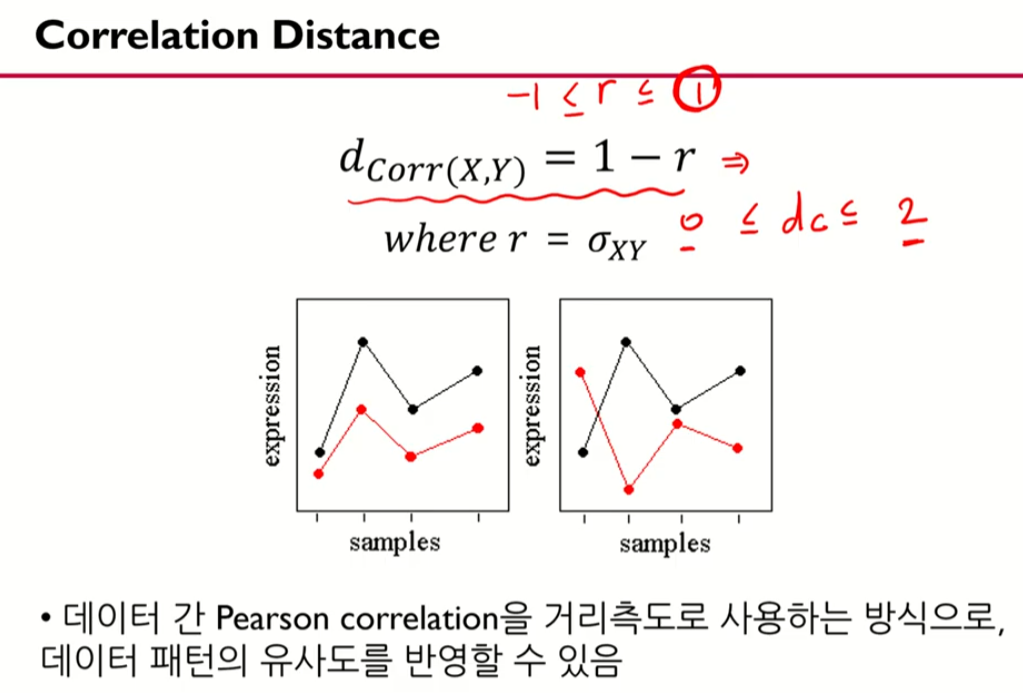
r = 상관계수
보통 전반적인 패턴을 봐야하는 데이터에서 자주 사용한다.
signal data로 보는 패턴에서 자주 사용!
유사할 수록 거리가 적음 (0에 가깝게 나옴)
유사하지 않을 수록 2에 가깝게
Spearman Rank Correlation

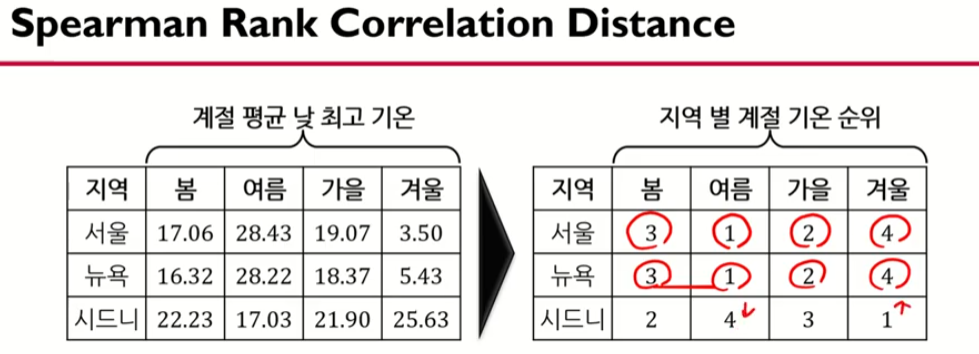
순위로 이루어진 데이터의 경우 거리를 측정할 때 Spearman Rank Correlation 이용

KNN의 장점과 한계점

KNN은 거리를 기반으로 하므로 고차원의 데이터는 불명확할 수 있다.
따라서 고차원이면 KNN이 잘 작동하지 않음
이 경우 차원을 줄여서 (차원축소) 해결한다.
Weighted KNN (가까운 것은 가중치를 크게, 먼 것은 적게)
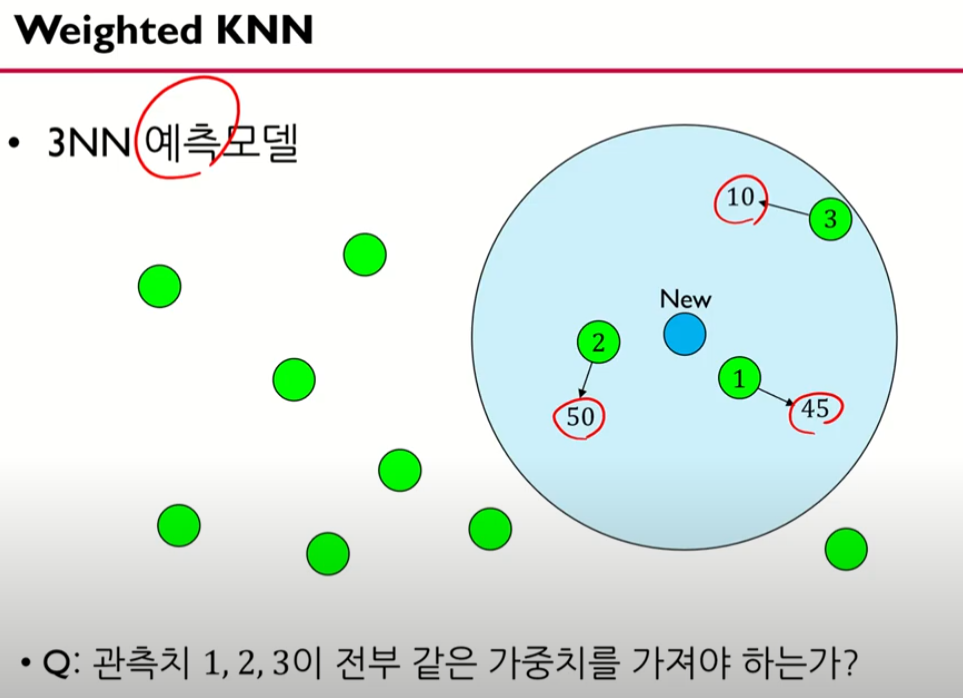
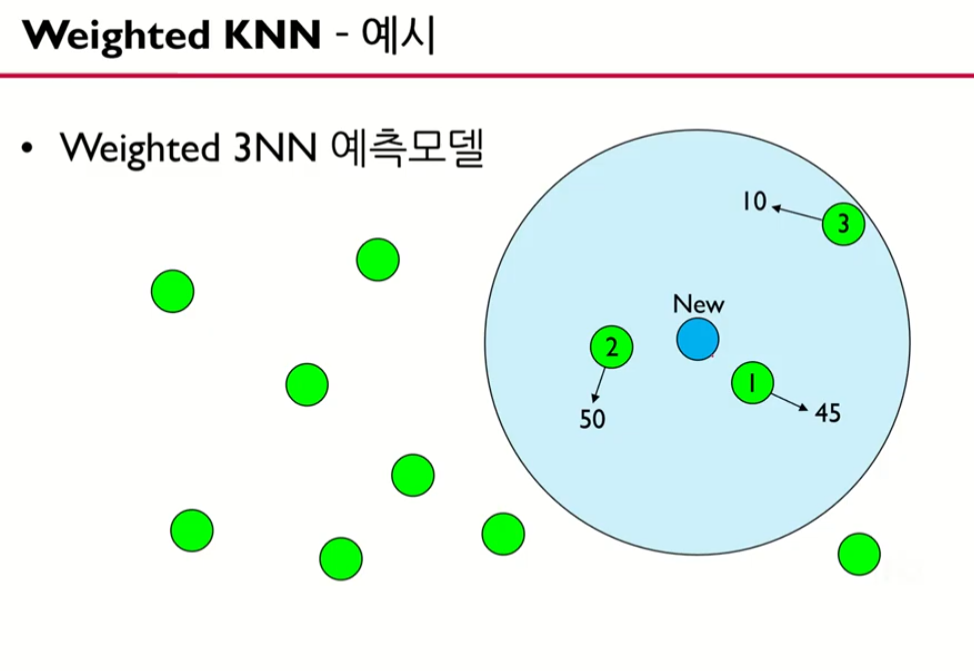
평균을 이용하는 것 보다는 가까운 것은 가중치를 크게, 먼 것은 가중치를 적게 두어야하지 않을까?
그러면 거리의 반비례를 고려하자.
웨이트를 고려하면
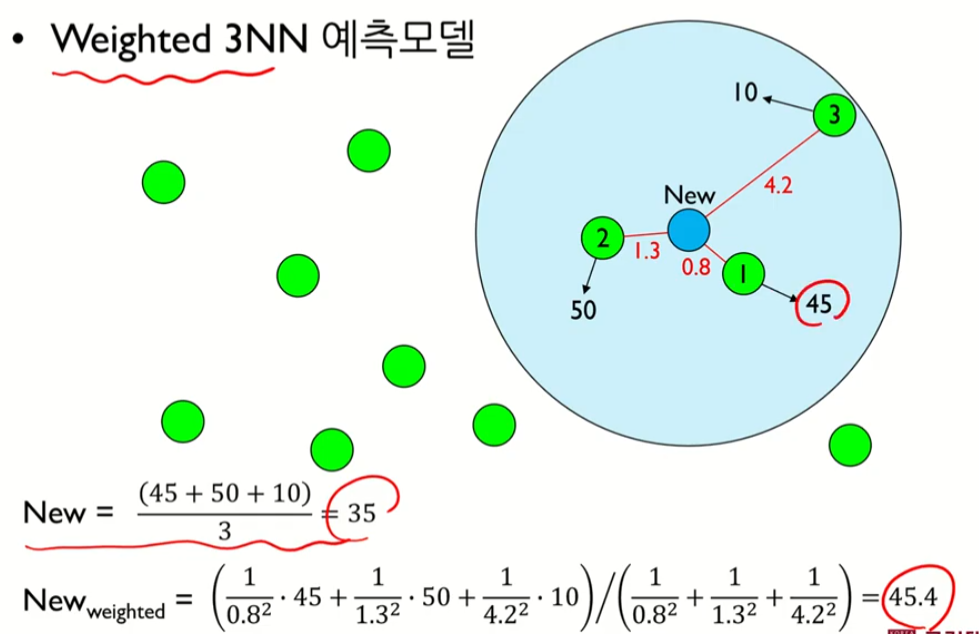
이런 식으로 가까운 것은 가중치가 크게 나타낼 수 이싿.
가중치 = 거리에 반비례함

가장 큰 값에 해당하는 argument, 범주를 정한다.
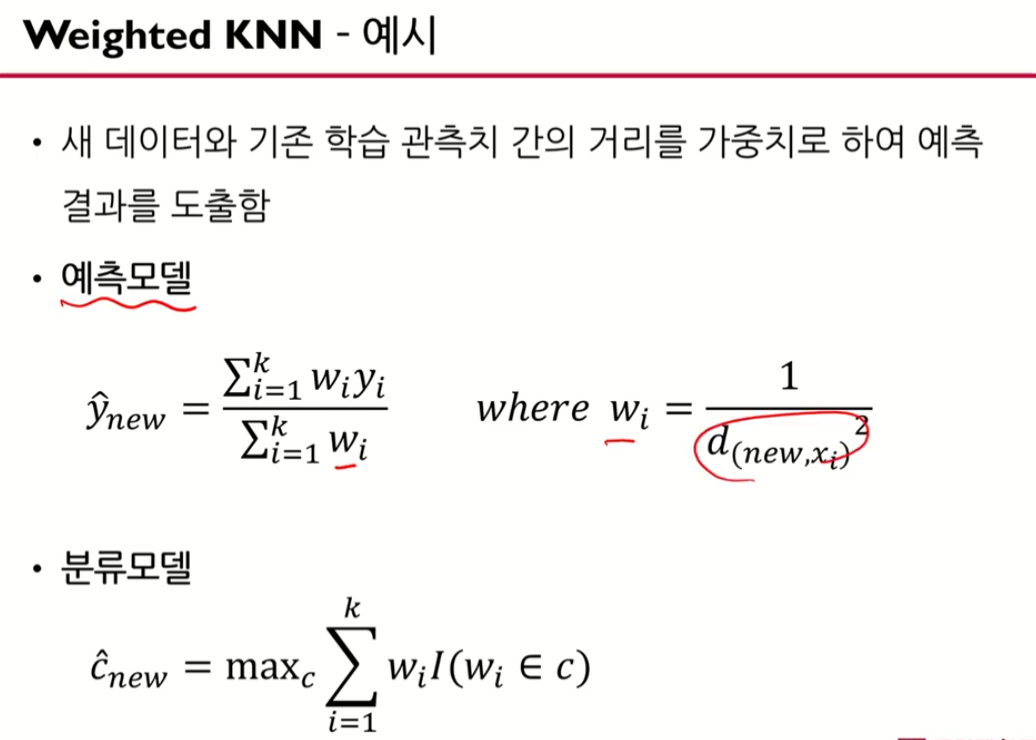
KNN 요약

'공부정리 > Deep learnig & Machine learning' 카테고리의 다른 글
| [핵심 머신러닝] 로지스틱회귀모델 1 (로지스틱함수, 승산) (0) | 2022.08.03 |
|---|---|
| [머신러닝] Mahalanobis Distance From Scratch in Python (0) | 2022.07.30 |
| [핵심 머신러닝] 선형회귀모델 4 (R2, ANOVA) - 강의 정리 (0) | 2022.07.22 |
| [핵심 머신러닝] 선형회귀모델 3 (파라미터 구간추정, 가설검정) - 강의 정리 (0) | 2022.07.22 |
| [핵심 머신러닝] 선형회귀모델 2 (파라미터 추정, 최소제곱법) - 강의 정리 (0) | 2022.07.22 |